오늘은 선형대수에서의 벡터에 대해서 다뤄보려 합니다.
벡터(Vector)의 정의
벡터는 magnitude(크기)와 direction(방향성)을 가진 수학적 물체입니다.
예시를 한 번 보겠습니다.
((\begin{bmatrix}
2\\
4\\
1
\end{bmatrix}))
위의 벡터는 3차원의 벡터로, 3차원 공간(( (R^3) ))에서의 한 점을 나타냅니다. 좌표 (( (0,0,0) )) 에서 (( (2,4,1) )) 로 가는 화살표를 생각해보면 좋을 것 같습니다.
벡터 간 덧셈
벡터 간의 덧셈은 다음과 같이 가능합니다.
((\begin{bmatrix}
3\\
4\\
5
\end{bmatrix} -
\begin{bmatrix}
1\\
2\\
3
\end{bmatrix}
=
\begin{bmatrix}
2\\
2\\
2
\end{bmatrix}))
같은 위치의 element들끼리 연산을 해주시면 됩니다.
벡터의 상수배
벡터에 상수(scalar)를 곱하여 벡터의 길이를 조정할 수 있습니다. 직관적으로는 어떤 벡터를 scale(늘이거나 줄인다)라고 받아들이면 될 것 같습니다. 마찬가지로 각각의 위치의 element들에게 곱셈을 하는 방식입니다. 예시는 다음과 같습니다.
((2\begin{bmatrix}
3\\
4\\
5
\end{bmatrix}
=
\begin{bmatrix}
6\\
8\\
10
\end{bmatrix}))
선형결합(Linear Combination)
벡터들은 선형결합을 시킬 수 있는데, 이는 벡터들에 스칼라 곱과 덧셈을 하여 만든, 벡터들의 결합을 의미합니다.
예시를 한 번 보겠습니다.
((2\begin{bmatrix}
3\\
4\\
5
\end{bmatrix}
-
3\begin{bmatrix}
1\\
2\\
3
\end{bmatrix}
=
\begin{bmatrix}
3\\
2\\
1
\end{bmatrix}))
선형독립과 종속(Linearly independent, Linearly dependent)
벡터들 간의 선형결합이 이루어질 때, Linear combination이 영벡터(Zero vector)가 되는 경우가 있는데, 이때 이 벡터들을 서로 linearly dependent하다고 합니다(선형종속).
예시를 보겠습니다.
((c\begin{bmatrix}
3\\
4\\
5
\end{bmatrix}
+
d\begin{bmatrix}
6\\
8\\
10
\end{bmatrix}))
위의 식에서 ((c = -2)) 이고 ((d = 1)) 일 때, 결과는 \begin{bmatrix}
0\\
0\\
0
\end{bmatrix}이 됩니다.
이렇게 결합하여 영벡터가 되는 경우들 중에, ((c)), ((d))가 둘 다 0인 경우에만 영벡터가 될 수 있다면(둘 다 0이면 그냥 없어지기에) Linearly independent한 것이고, 위의 경우처럼 0이 아님에도 영벡터가 결과로 나온다면 Linearly dependent한 것입니다. 예컨대, 다른 하나의 벡터에 0을 제외하고 무슨 짓을 해도 그 다른 벡터를 만들지 못할 때 독립인 것입니다.
좀 더 직관적으로, 벡터를 시각화해보겠습니다.

빨간색 벡터가 ((\begin{bmatrix}
3\\
4\\
5
\end{bmatrix}))이고 파란색 벡터가 ((\begin{bmatrix}
6\\
8\\
10
\end{bmatrix})) 입니다. 현재 두 벡터가 완전히 겹쳐서 이 둘을 아무리 늘이거나 줄이거나, 서로 더하거나 빼거나 해도 하나의 선 위에서만 노는 모습을 볼 수 있습니다. 벡터 간의 Linear combination으로 만들 수 있는 모든 조합들을 Span이라고 합니다. 위 그림에서 마찬가지로 ((\begin{bmatrix}
3\\
4\\
5
\end{bmatrix}))와 ((\begin{bmatrix}
6\\
8\\
10
\end{bmatrix}))를 아무리 늘리고 줄이고 상수배를 해서 더해도(선형결합) 저 직선 안에서 벗어나지 못합니다. 그러므로 이 두 벡터들의 Span은 Line이며, 3차원에서 두 벡터를 선형결합했음에도 불구하고 그 Span이 line인 것으로 보아 dependent한 관계에 있다고 설명할 수 있습니다. 실제로 ((\begin{bmatrix}
3\\
4\\
5
\end{bmatrix}))를 2배 하면 ((\begin{bmatrix}
6\\
8\\
10
\end{bmatrix}))를 만들 수 있다는 것을 바로 알 수 있습니다.
Linearly independent한 경우를 보겠습니다.
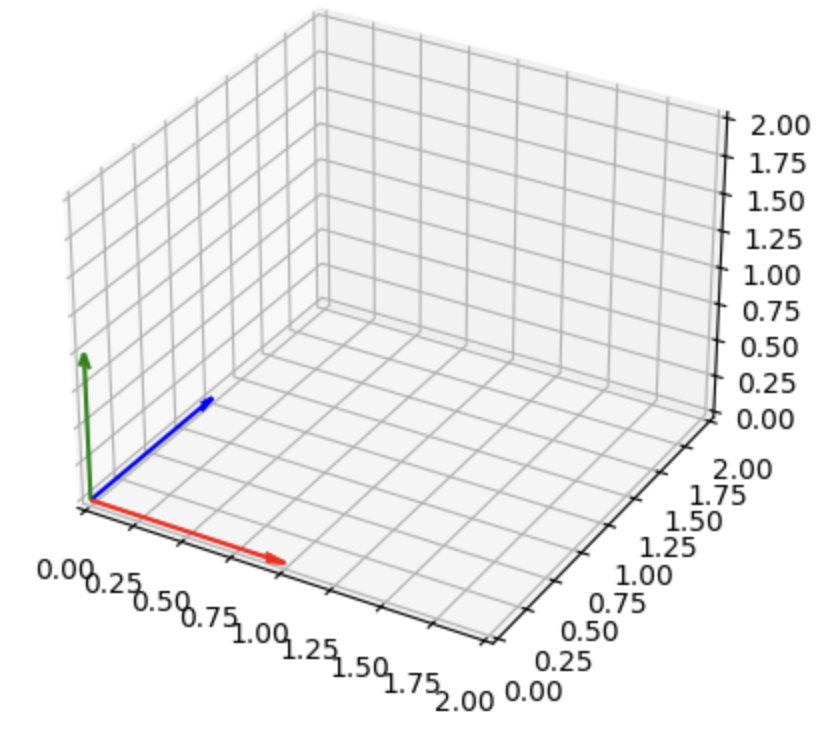
이번에는 ((\begin{bmatrix}
1\\
0\\
0
\end{bmatrix})),((\begin{bmatrix}
0\\
1\\
0
\end{bmatrix})),((\begin{bmatrix}
0\\
0\\
1
\end{bmatrix})), 이렇게 3개의 벡터를 시각화하였습니다. 이 세 개의 벡터들은 각각 서로 다른 축에 위치해있으며, 3차원 공간을 이루는 근간인 x축, y축, z축입니다. 이 3개의 벡터는 서로 겹치지 않으며, 이들을 상수배하여 더한다고 해도 하나의 직선을 만들 수는 없습니다. 그렇기 때문에 이 3개의 벡터들을 이용한 모든 조합들을 구해본다면 ((R^3))을 이룰 것입니다. 결국, ((c \begin{bmatrix}
1\\
0\\
0
\end{bmatrix})) + ((d \begin{bmatrix}
0\\
1\\
0
\end{bmatrix})) + ((e \begin{bmatrix}
0\\
0\\
1
\end{bmatrix}))에서 모든 ((c)), ((d)), ((e))는 3차원 공간을 메웁니다. 3차원 공간에서 3개의 벡터들이 3차원 공간을 만드니, 이들은 서로 Linearly independent하다고 할 수 있습니다.
종합적으로 정리하자면, ((c))((v)) + ((d))((w)) + ((e))((z))는 ((v)), ((w)), ((z))가 선형독립일 때 3차원 공간을 메운다고 생각하시면 될 것 같습니다.
내적(Dot product)
Dot product는 내적이라고도 하고 스칼라곱이라고도 합니다. 이는 두 벡터를 이용해 하나의 스칼라를 얻는 연산이라는 의미입니다.
예시를 보겠습니다.
((v)) ((\cdot)) ((w)) = ((\begin{bmatrix}
3\\
4\\
5
\end{bmatrix})) ((\cdot)) ((\begin{bmatrix}
2\\
0\\
1
\end{bmatrix})) ((= 11))
((v))와 ((w)) 두 벡터가 존재할 때 ((3))x((2)) + ((4))x((0)) + ((5))x((1)) = ((11)) 이런 방식으로 게산하여 하나의 스칼라값을 얻습니다.
내적의 성질 중 하나는 ((v)) ((\cdot)) ((w)) = ((w)) ((\cdot)) ((v))와 같이 교환법칙(Commutative law)가 성립한다는 것입니다.
내적을 통하여 구할 수 있는 것들 중에서는 길이와 각도가 있습니다.
벡터의 길이(Euclidean/2-norms)
어떤 벡터를 자기 자신과 내적을 취하면 벡터의 길이를 구할 수 있습니다.
(( \left \| v \right \|^{2} )) = ((v)) ((\cdot)) ((v)) = ((\begin{bmatrix}
3\\
4\\
5
\end{bmatrix})) ((\cdot)) ((\begin{bmatrix}
3\\
4\\
5
\end{bmatrix})) (( = 9 + 16 + 25 ))
그리고 벡터의 길이가 1인 벡터를 unit vector라고 합니다.
((u = \frac{v}{\left \| v \right \|}))
두 벡터 간 각도(Angles)
두 벡터 간의 dot product ((v \cdot w))를 통해 벡터 v와 w 사이의 각도 ((\theta))를 알 수 있습니다.
이는 벡터의 내적에서 가장 중요한 성질이라고 말할 수 있을 것 같은데, 후에 어떤 벡터와 다른 벡터의 유사성 정도를 각도로 알아낼 수 있기 때문입니다.
(( v\cdot w = \left \| v \right \|\left \| w \right \| cos \theta ))
예시를 보여드리겠습니다.
((v)) = ((\begin{bmatrix}
2\\
2\\
-1
\end{bmatrix})), ((w)) = ((\begin{bmatrix}
-1\\
2\\
2
\end{bmatrix})) 일 때 ((\theta)) = 90° 입니다. 왜냐하면 내적을 계산해보면 ((2))x((-1)) + ((2))x((2)) + ((-1))x((2)) = ((0))이고, ((cos 90° ))가 0이기 때문입니다. 따라서 어떤 두 벡터를 내적하였을 때 0이 나온다는 뜻은, 두 벡터가 직교한다는 뜻입니다.
그림으로 본다면,

실제로 직각인 모습을 볼 수 있습니다.
'Linear Algebra' 카테고리의 다른 글
| 행렬의 곱셈(Matrix-Matrix Multiplication) (0) | 2024.01.17 |
|---|---|
| 행렬(Matrix)의 Rank (0) | 2024.01.16 |
| 행렬(Matrix) - Column space & Row space (0) | 2024.01.16 |
| 행렬은 선형변환이다. (0) | 2024.01.16 |
| [선형대수] 행렬(Matrix)의 기초 (0) | 2024.01.16 |
