안녕하세요, 오늘은 그람-슈미트 과정을 직접적으로 다루기 전 그람-슈미트를 왜 하는지와, 직교성과 Orthonomal에 대해서 설명해보려고 합니다. 그람-슈미트 과정은, 이를 왜 하는지에 대한 이유와 필요한 개념들을 설명하기 위한 part 1과, 직접 계산을 해보는 part 2로 나누어서 다뤄볼 것입니다.
반드시 직전의 게시물을 보고 오시는 것을 추천드립니다.
https://jaehoonstudy.tistory.com/21
부분공간에 벡터 투영시키기(Projection onto Subspaces)
오늘은 벡터를 부분공간에 project하는 방법에 대해서 알아보도록 하겠습니다. 지난 게시물인 '직교성과 부분공간' 의 마지막 부분에 이어서 진행해보도록 하겠습니다. https://jaehoonstudy.tistory.com/20
jaehoonstudy.tistory.com
또한 직교성에 대한 게시물도 참고해보면 좋을 것 같습니다.
https://jaehoonstudy.tistory.com/20
직교성(Orthogonality)과 부분공간(Subspaces)
오늘은 직교하는 벡터들과 부분공간들에 대해서 간단히 다뤄보도록 하겠습니다. 직교하는 성질은 공학에서도 중요한 성질입니다. 직교성(Orthogonality)가 충족된다면, 독립(independence)를 보장해주
jaehoonstudy.tistory.com
Normal Equation
우리가 지금 처해있는 상황은 ((A))((x)) ((=)) ((b))인 상황에서 해가 없을 때를 다루고 있습니다. 해가 없는 이유는 ((A))((x)) ((=)) ((b))인 상황에서 해가 있으려면 ((b))가 ((A))의 column space 위에 존재해야합니다. 그런데 ((b))가 column space 위에 위치하지 않으니, ((b)) 벡터에 투영행렬을 곱해주어 column space에 투영해준 뒤(끌어내린 뒤), 이를 만족하는 가장 근사해인 ((\hat{x}))를 구해주자는 것입니다.
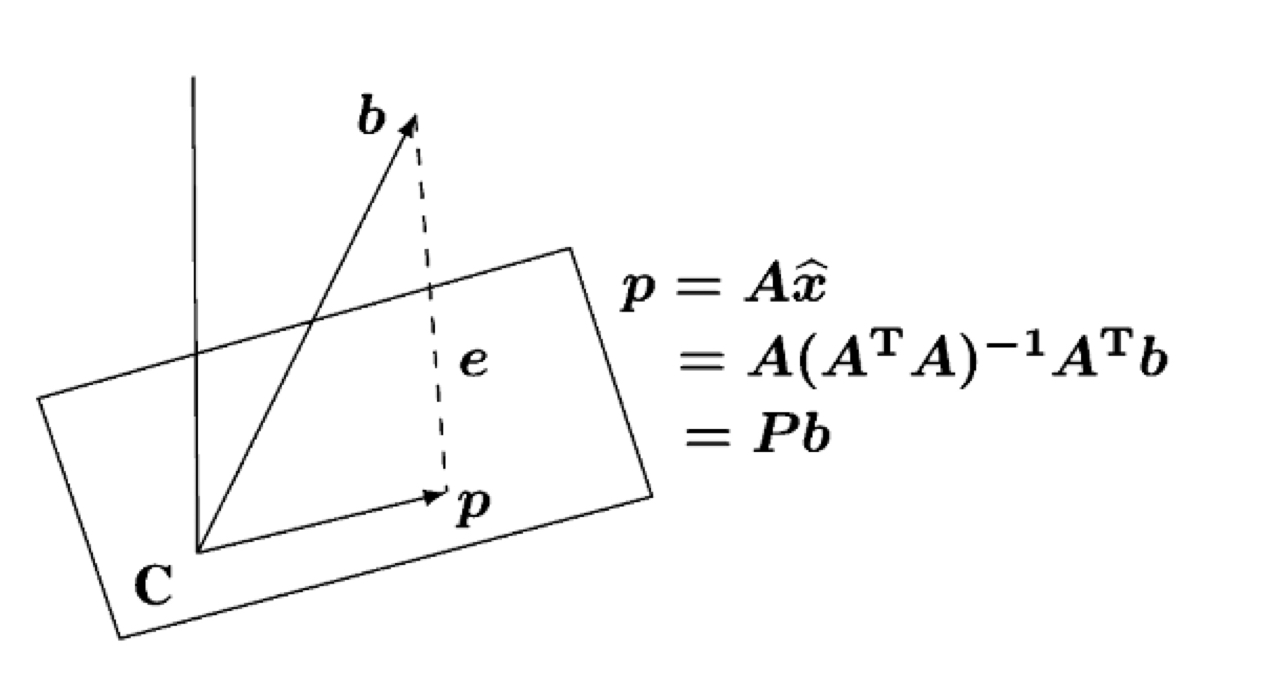
이렇게 ((b))가 ((C))인 column space 위에 없으므로, ((b))를 subspace에 투영하여((p))로 만들어 준 뒤, 근사해인 ((\hat{x}))를 구해주자는 것이 바로 그 배경입니다.
그렇다면 근사해인 ((\hat{x}))을 구하려면 가장 중요한 식은 무엇일까요? 바로 Normal Equation입니다.

이전 게시물에서 설명을 했지만, ((b)) ((=)) ((p)) ((=)) ((e))인 점을 이용하여 유도되는데, ((e))와 column space가 직교한다는 사실을 이용합니다. ((e))를 ((b)) ((-)) ((p))로 표현하고, ((A))와 내적하면 0이 된다는 사실을 이용합니다(직교성).
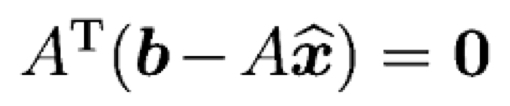
이걸 다시 정리하면 위의 Normal Equation의 형태가 됩니다.
결국 근사해인 ((\hat{x}))를 구하기 위해서 해야할 일은 이 Normal Equation을 푸는 일입니다. 이어질 Gram-schmidt 과정도 이 Normal equation을 어떻게 하면 쉽게 풀지에 대한 방법론이라고 할 수 있습니다.
((A^{T}))((A))의 invertibility(가역성)
Invertibility는 역행렬이 존재하는가를 묻는 문제입니다. 우리가 ((\hat{x}))를 구하기 위해서는 좌변에 ((\hat{x}))만 남기고 다 넘겨주면 됩니다. 그렇게 하기 위해서는 ((A^{T}))((A))의 역을 우변에 곱해주어야합니다. 그런데 모든 행렬이 역행렬이 존재하는 것은 아닙니다.

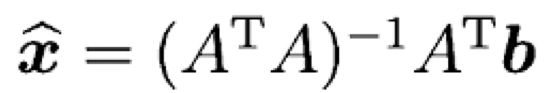
여기서 중요한 개념이 나오는데, ((A))의 모든 column들이 independent할 경우, ((A^{T}))((A))도 invertible하다는 것입니다. 증명은 생략하도록 하겠습니다.
Orthonormal(정규직교) - 어떨 때 column이 확실히 independent한가?
이것이 바로 그람-슈미트 과정의 빌드업인데요, 위에서 ((A))의 모든 column들이 independent할 경우가 중요하다고 하였습니다.
어떨 때 column들이 확실하게 independent할까요?
만약 column들이 직교하는 단위벡터들이라면 무조건 독립입니다.
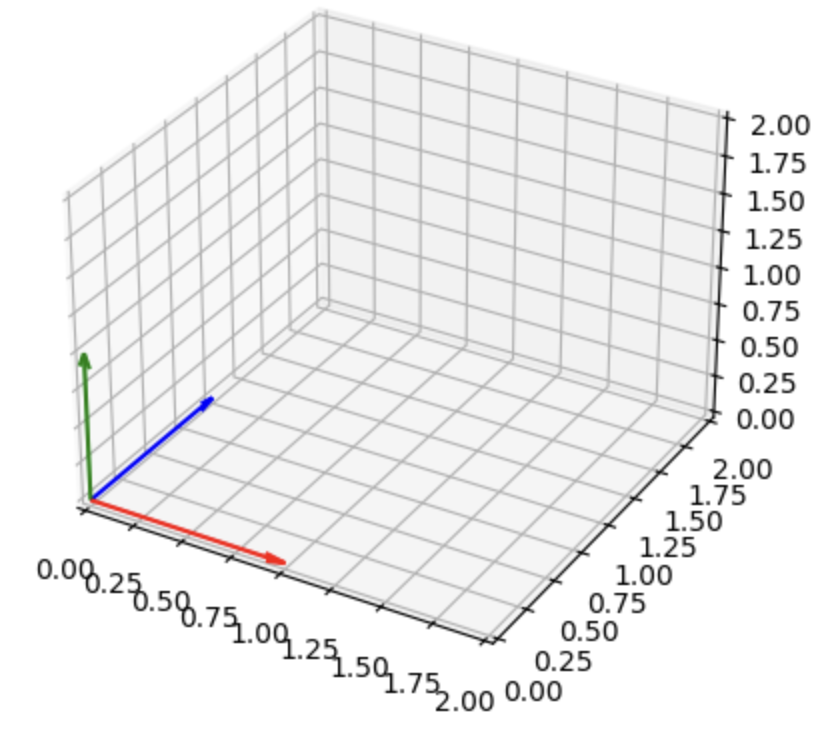
이렇게 말이죠.
직교하는데 벡터들이 unit vector(길이가 1인 벡터) 일 경우, 이를 Orthonormal하다고 표현합니다.
Orthonormal Basis
Orthonomal한 벡터들로 column이 구성된, orthonormal한 basis들을 가진 행렬을 보겠습니다.
Orthonormal한 벡터들을 ((q_i)), ((q_j)) 이렇게 표현해보겠습니다. 이들은 직교하기 때문에 내적하면 0이 나올 것입니다. 이들을 내적한다면 이렇게 됩니다.
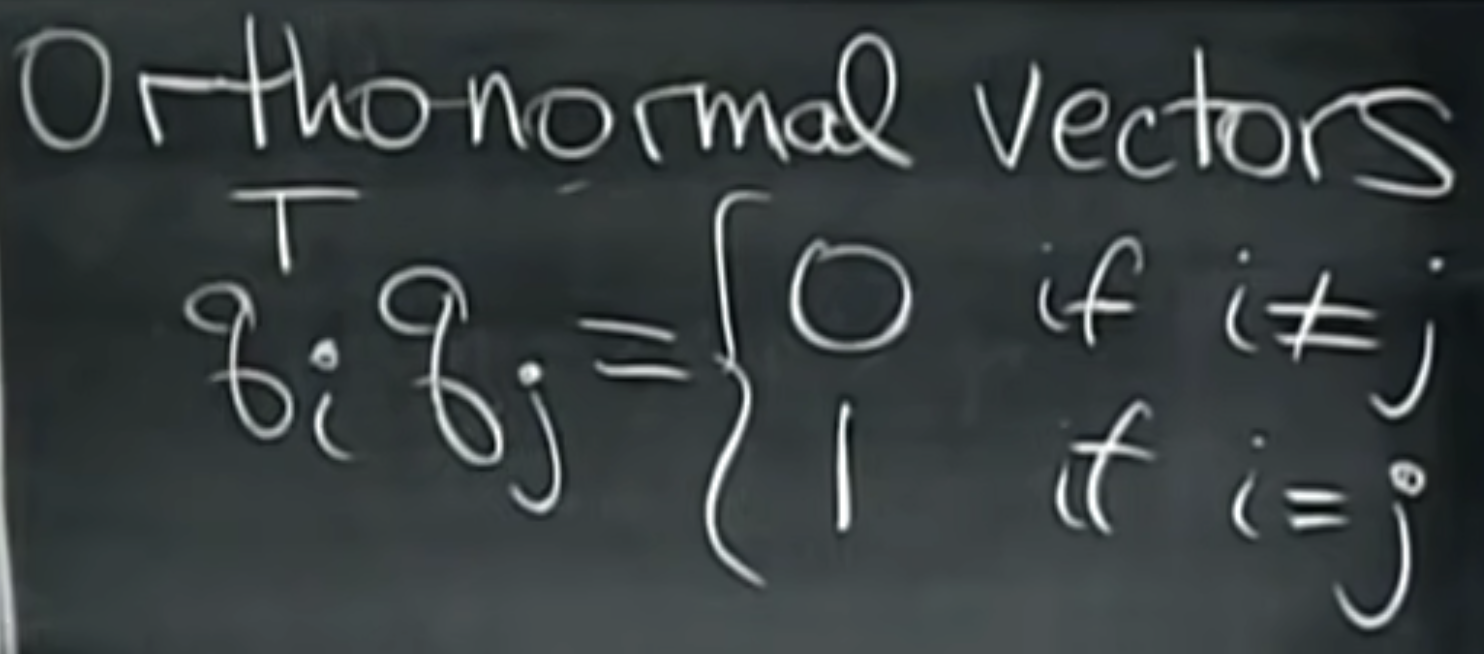
0이 될 수도 있고 1이 될 수도 있는데, 자기 자신과 내적하면 1이 되고(원래 길이가 1이었으니), 다른 벡터와 내적하면 직교하는 관계이므로 0이 되는 것입니다.
왜 이렇게 되는지 그림으로 보자면, ((Q^{T}))((Q))를 표현해보면 다음과 같습니다.
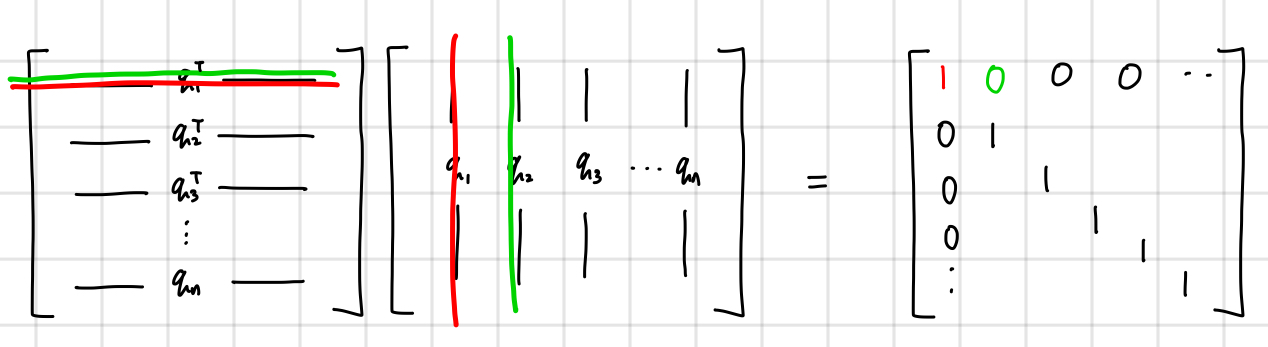
이를 개별 벡터인 ((q^{T}))와 ((q))로 나눠서 생각해보고 곱해보면 이렇게 Identity가 나옵니다.
또 중요한 개념이 나오는데, orthonormal한 ((Q))가 정방행렬일 때 ((Q^{T}))((Q)) ((=)) ((I)) 가 된다는 것입니다.
그런데 우리는 둘이 곱해서 Identity가 나오는 것을 어디선가 본 적이 있습니다. 바로 어떤 행렬과 그 역행렬을 곱해주면 Identity가 나온다는 것입니다. 그렇기 때문에 orthonormal한 ((Q))의 transpose는 ((Q))의 inverse와 같다는 사실을 도출할 수 있습니다.
orthonormal한 정방행렬 ((Q))가 있을 때 ((Q^{-1})) = ((Q^{T}))이다.
왜 ((Q))가 좋은가?
왜 Q가 좋을까요? 다시 우리의 Normal Equation이랑, 근사해인 ((\hat{x}))을 구하기 위해 사용한 식들로 되돌아가봅시다.
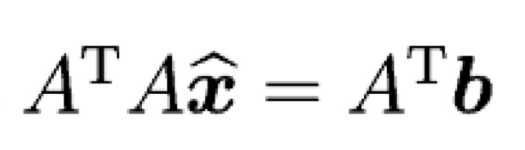
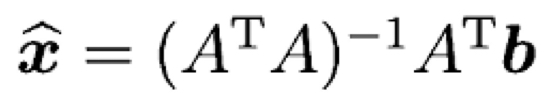
우리는 앞선 벡터의 투영 게시물에서 ((b))에 투영행렬(projection matrix)를 곱하여 최종적으로 투영된 결과물을 알 수 있다고 했습니다.
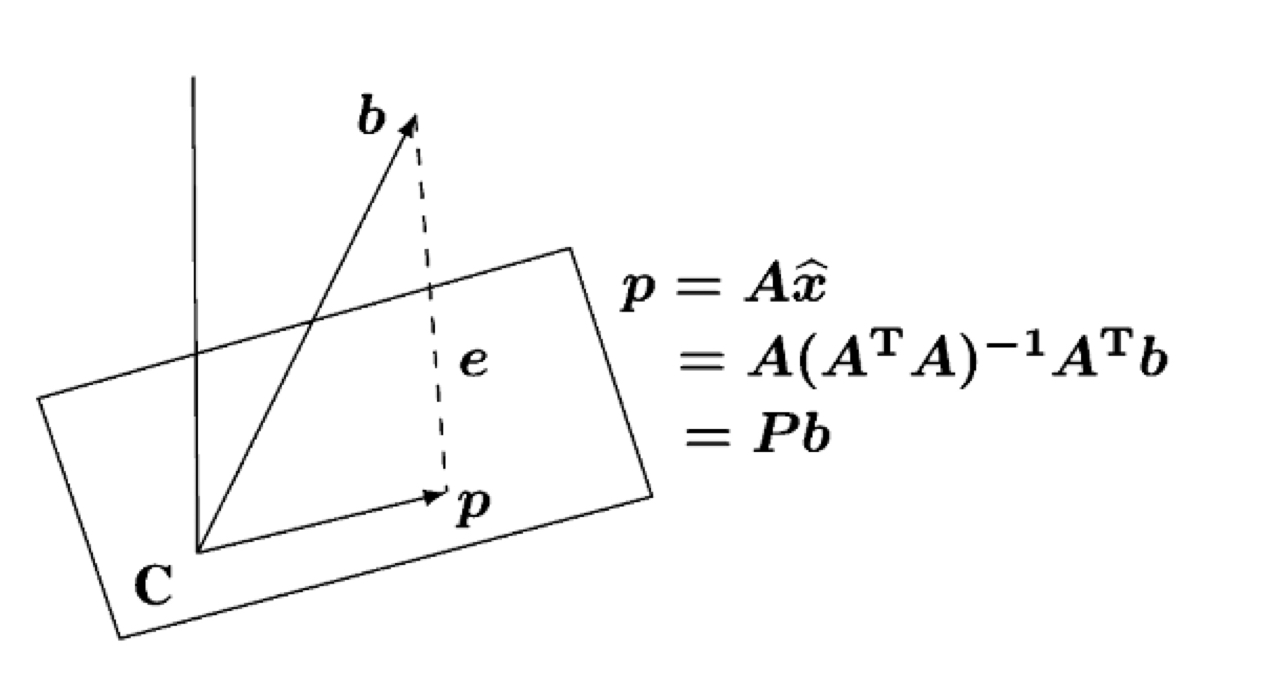
그렇다면 우리의 projection matrix는 ((b)) 앞에 있는 식이 됩니다.
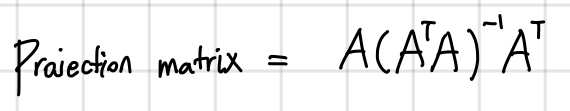
이게 만약 ((Q))라고 생각해볼까요?
아까 ((Q^{T})((Q)) = ((I)) 인 성질이 있다고 했습니다. 그러면 중간의 inverse term은 없어지고, 최종적으로 ((Q))((Q^{T}))만 남을 것입니다!

무엇보다 중요한 것은,
우리의 근사해인 ((\hat{x}))를 구하기 위한 Normal Equation으로 돌아가서, ((A))가 ((Q))라고 생각해봅시다.
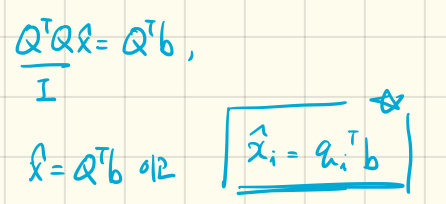
우리는 근사해인 ((\hat{x}))를 귀찮은 inverse 연산 없이 그저 내적 한 번으로 구할 수 있게 되는 것입니다!
정리
이런 식으로 선형대수에서는 힘든 계산인 inverse 계산을 줄이기 위해서 고안되는 기법들이 많습니다. Gram-Schmidt process도 그 중 하나이며, ((A))를 ((Q))로 바꿔주는 변형을 통해 근사해를 매우 간단하게 구할 수 있다는 것에 그 의의가 있습니다. 이제 ((A))를 ((Q))로 바꿔주는 작업인 Gram-Schmidt 과정에 대해서 다음에 다루어보도록 하겠습니다.
'선형대수' 카테고리의 다른 글
| 부분공간에 벡터 투영시키기(Projection onto Subspaces) (0) | 2024.02.16 |
|---|---|
| 직교성(Orthogonality)과 부분공간(Subspaces) (1) | 2024.01.31 |
| Solving ((A))((x)) ((=)) ((b)) (When ((m)) < ((n))) (2) | 2024.01.30 |
| 선형연립방정식의 해의 존재성 (1) | 2024.01.30 |
| Gauss-Jordan Elimination(가우스-조던 소거법) & RREF (1) | 2024.01.29 |
안녕하세요, 오늘은 그람-슈미트 과정을 직접적으로 다루기 전 그람-슈미트를 왜 하는지와, 직교성과 Orthonomal에 대해서 설명해보려고 합니다. 그람-슈미트 과정은, 이를 왜 하는지에 대한 이유와 필요한 개념들을 설명하기 위한 part 1과, 직접 계산을 해보는 part 2로 나누어서 다뤄볼 것입니다.
반드시 직전의 게시물을 보고 오시는 것을 추천드립니다.
https://jaehoonstudy.tistory.com/21
부분공간에 벡터 투영시키기(Projection onto Subspaces)
오늘은 벡터를 부분공간에 project하는 방법에 대해서 알아보도록 하겠습니다. 지난 게시물인 '직교성과 부분공간' 의 마지막 부분에 이어서 진행해보도록 하겠습니다. https://jaehoonstudy.tistory.com/20
jaehoonstudy.tistory.com
또한 직교성에 대한 게시물도 참고해보면 좋을 것 같습니다.
https://jaehoonstudy.tistory.com/20
직교성(Orthogonality)과 부분공간(Subspaces)
오늘은 직교하는 벡터들과 부분공간들에 대해서 간단히 다뤄보도록 하겠습니다. 직교하는 성질은 공학에서도 중요한 성질입니다. 직교성(Orthogonality)가 충족된다면, 독립(independence)를 보장해주
jaehoonstudy.tistory.com
Normal Equation
우리가 지금 처해있는 상황은 ((A))((x)) ((=)) ((b))인 상황에서 해가 없을 때를 다루고 있습니다. 해가 없는 이유는 ((A))((x)) ((=)) ((b))인 상황에서 해가 있으려면 ((b))가 ((A))의 column space 위에 존재해야합니다. 그런데 ((b))가 column space 위에 위치하지 않으니, ((b)) 벡터에 투영행렬을 곱해주어 column space에 투영해준 뒤(끌어내린 뒤), 이를 만족하는 가장 근사해인 ((\hat{x}))를 구해주자는 것입니다.

이렇게 ((b))가 ((C))인 column space 위에 없으므로, ((b))를 subspace에 투영하여((p))로 만들어 준 뒤, 근사해인 ((\hat{x}))를 구해주자는 것이 바로 그 배경입니다.
그렇다면 근사해인 ((\hat{x}))을 구하려면 가장 중요한 식은 무엇일까요? 바로 Normal Equation입니다.

이전 게시물에서 설명을 했지만, ((b)) ((=)) ((p)) ((=)) ((e))인 점을 이용하여 유도되는데, ((e))와 column space가 직교한다는 사실을 이용합니다. ((e))를 ((b)) ((-)) ((p))로 표현하고, ((A))와 내적하면 0이 된다는 사실을 이용합니다(직교성).
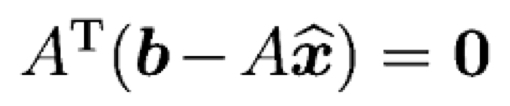
이걸 다시 정리하면 위의 Normal Equation의 형태가 됩니다.
결국 근사해인 ((\hat{x}))를 구하기 위해서 해야할 일은 이 Normal Equation을 푸는 일입니다. 이어질 Gram-schmidt 과정도 이 Normal equation을 어떻게 하면 쉽게 풀지에 대한 방법론이라고 할 수 있습니다.
((A^{T}))((A))의 invertibility(가역성)
Invertibility는 역행렬이 존재하는가를 묻는 문제입니다. 우리가 ((\hat{x}))를 구하기 위해서는 좌변에 ((\hat{x}))만 남기고 다 넘겨주면 됩니다. 그렇게 하기 위해서는 ((A^{T}))((A))의 역을 우변에 곱해주어야합니다. 그런데 모든 행렬이 역행렬이 존재하는 것은 아닙니다.

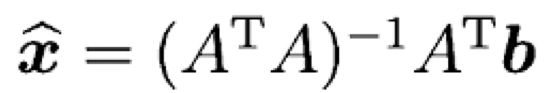
여기서 중요한 개념이 나오는데, ((A))의 모든 column들이 independent할 경우, ((A^{T}))((A))도 invertible하다는 것입니다. 증명은 생략하도록 하겠습니다.
Orthonormal(정규직교) - 어떨 때 column이 확실히 independent한가?
이것이 바로 그람-슈미트 과정의 빌드업인데요, 위에서 ((A))의 모든 column들이 independent할 경우가 중요하다고 하였습니다.
어떨 때 column들이 확실하게 independent할까요?
만약 column들이 직교하는 단위벡터들이라면 무조건 독립입니다.

이렇게 말이죠.
직교하는데 벡터들이 unit vector(길이가 1인 벡터) 일 경우, 이를 Orthonormal하다고 표현합니다.
Orthonormal Basis
Orthonomal한 벡터들로 column이 구성된, orthonormal한 basis들을 가진 행렬을 보겠습니다.
Orthonormal한 벡터들을 ((q_i)), ((q_j)) 이렇게 표현해보겠습니다. 이들은 직교하기 때문에 내적하면 0이 나올 것입니다. 이들을 내적한다면 이렇게 됩니다.
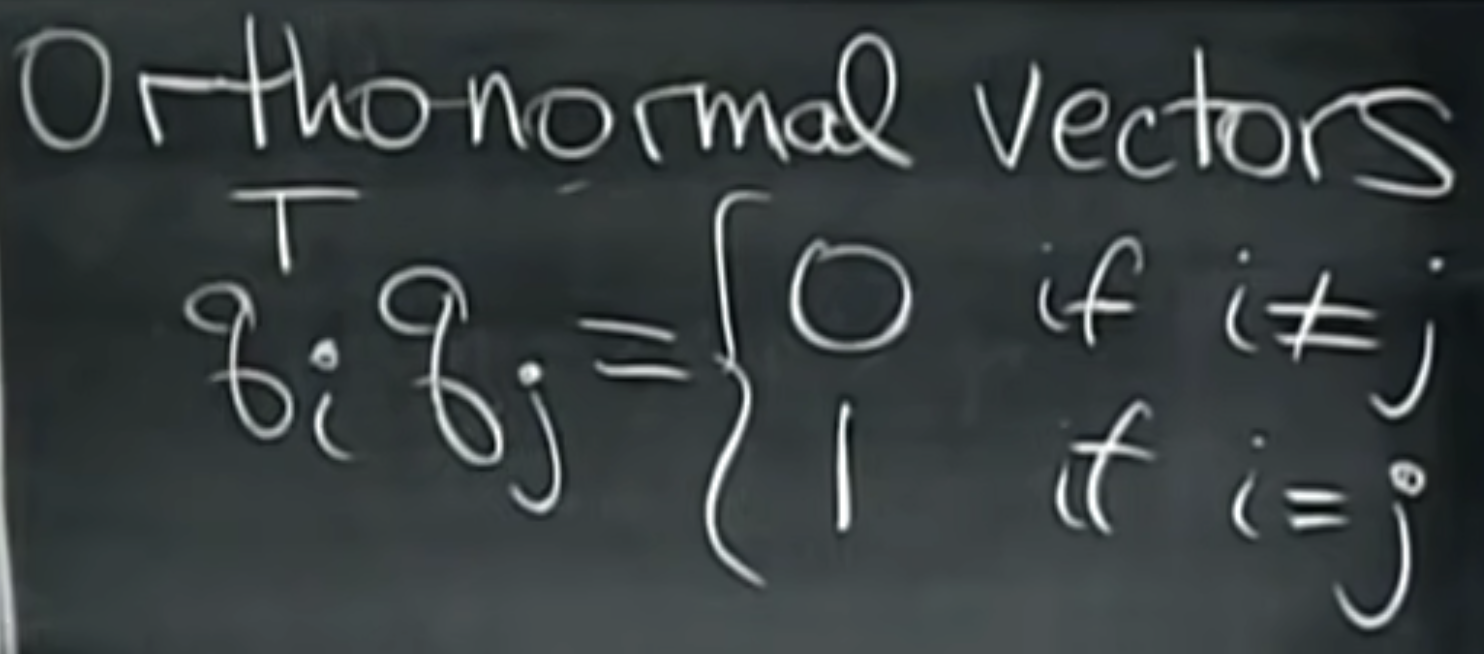
0이 될 수도 있고 1이 될 수도 있는데, 자기 자신과 내적하면 1이 되고(원래 길이가 1이었으니), 다른 벡터와 내적하면 직교하는 관계이므로 0이 되는 것입니다.
왜 이렇게 되는지 그림으로 보자면, ((Q^{T}))((Q))를 표현해보면 다음과 같습니다.

이를 개별 벡터인 ((q^{T}))와 ((q))로 나눠서 생각해보고 곱해보면 이렇게 Identity가 나옵니다.
또 중요한 개념이 나오는데, orthonormal한 ((Q))가 정방행렬일 때 ((Q^{T}))((Q)) ((=)) ((I)) 가 된다는 것입니다.
그런데 우리는 둘이 곱해서 Identity가 나오는 것을 어디선가 본 적이 있습니다. 바로 어떤 행렬과 그 역행렬을 곱해주면 Identity가 나온다는 것입니다. 그렇기 때문에 orthonormal한 ((Q))의 transpose는 ((Q))의 inverse와 같다는 사실을 도출할 수 있습니다.
orthonormal한 정방행렬 ((Q))가 있을 때 ((Q^{-1})) = ((Q^{T}))이다.
왜 ((Q))가 좋은가?
왜 Q가 좋을까요? 다시 우리의 Normal Equation이랑, 근사해인 ((\hat{x}))을 구하기 위해 사용한 식들로 되돌아가봅시다.
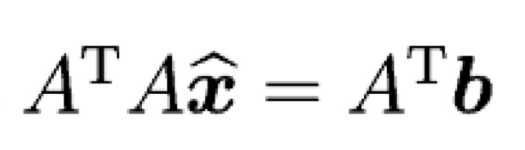
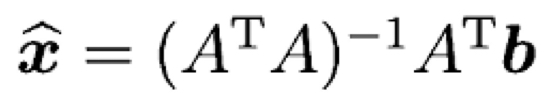
우리는 앞선 벡터의 투영 게시물에서 ((b))에 투영행렬(projection matrix)를 곱하여 최종적으로 투영된 결과물을 알 수 있다고 했습니다.

그렇다면 우리의 projection matrix는 ((b)) 앞에 있는 식이 됩니다.
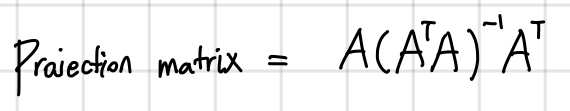
이게 만약 ((Q))라고 생각해볼까요?
아까 ((Q^{T})((Q)) = ((I)) 인 성질이 있다고 했습니다. 그러면 중간의 inverse term은 없어지고, 최종적으로 ((Q))((Q^{T}))만 남을 것입니다!

무엇보다 중요한 것은,
우리의 근사해인 ((\hat{x}))를 구하기 위한 Normal Equation으로 돌아가서, ((A))가 ((Q))라고 생각해봅시다.

우리는 근사해인 ((\hat{x}))를 귀찮은 inverse 연산 없이 그저 내적 한 번으로 구할 수 있게 되는 것입니다!
정리
이런 식으로 선형대수에서는 힘든 계산인 inverse 계산을 줄이기 위해서 고안되는 기법들이 많습니다. Gram-Schmidt process도 그 중 하나이며, ((A))를 ((Q))로 바꿔주는 변형을 통해 근사해를 매우 간단하게 구할 수 있다는 것에 그 의의가 있습니다. 이제 ((A))를 ((Q))로 바꿔주는 작업인 Gram-Schmidt 과정에 대해서 다음에 다루어보도록 하겠습니다.
'선형대수' 카테고리의 다른 글
| 부분공간에 벡터 투영시키기(Projection onto Subspaces) (0) | 2024.02.16 |
|---|---|
| 직교성(Orthogonality)과 부분공간(Subspaces) (1) | 2024.01.31 |
| Solving ((A))((x)) ((=)) ((b)) (When ((m)) < ((n))) (2) | 2024.01.30 |
| 선형연립방정식의 해의 존재성 (1) | 2024.01.30 |
| Gauss-Jordan Elimination(가우스-조던 소거법) & RREF (1) | 2024.01.29 |
