저번 게시물에서 해의 존재성에 대해 자세히 다뤘었습니다. 이번에는 드디어 해가 존재할 때, 이를 어떻게 푸는지 알아보도록 하겠습니다. 이전에는 ((A))가 ((m)) = ((n))이고 dependent한 column이 없는 특수한 경우만 다뤘었다면, 이제는 이를 일반화 시켜서 해가 존재할 때, ((A)) 내에 dependent한 column들이 있을 때도, ((A))가 ((m)) = ((n))인 정방행렬(square matrix)이 아닐 때도 통하는 방법에 대해서 다루는 것입니다.
((A))((x)) ((=)) ((b))의 complete solution을 구하는 방법
저번 게시물인 해의 존재성에 대한 게시물을 보시지 않으셨다면, 이를 반드시 보고 오시는 것을 추천드립니다.
https://jaehoonstudy.tistory.com/18
선형연립방정식의 해의 존재성
오늘은, 우리가 푸는 문제인, ((A))((x)) ((=)) ((b)) 를 풀기 전 확인해야하는 해의 존재성에 대해서 알아보도록 하겠습니다. 해가 유일할 때, 없을 때, 무한할 때와 그에 따른 ((A))의 모양과 함꼐 연관
jaehoonstudy.tistory.com
그리고 rref에 대해서도 한 번 다시 보시고 오는 것을 추천드립니다.
https://jaehoonstudy.tistory.com/17
Gauss-Jordan Elimination(가우스-조던 소거법) & RREF
오늘은 이전 게시물에서 다루었던 부분공간들을 발견할 수 있는, 그리고 이후 문제 해결에서 도움이 되는 가우스-조던 소거법과, rref(기약 행사다리꼴)에 대해서 알아보도록 하겠습니다. Gauss-Jor
jaehoonstudy.tistory.com
지금 다루는 경우가 어떤 경우인가?
일단 지금 다루려는 경우, 지금 아래에 서술할 방법론이 어떤 경우에 쓰이는 방법인지 명확하게 인지하고 넘어갈 필요가 있습니다.
선형방정식계에서 매우 크게 경우의 수를 분류하면, 해가 존재할 수도 있고 존재하지 않을 수도 있습니다. 해의 존재성 게시물에서 보셨겠지만, 경우는 다음과 같습니다.
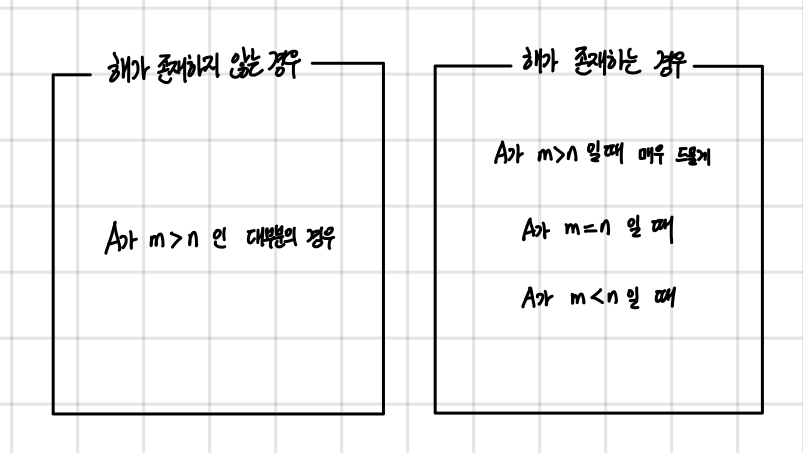
A가 ((m)) > ((n))일 때는, 매우 드물게 ((b))가 ((A))의 column space 내에 존재하는 경우에 해가 있습니다.
지금 중점적으로 다루려는 경우는 해가 존재할 때, 즉 ((A))가 정방행렬인데 dependent column이 있을 때, 그리고 ((A))가 ((m)) < ((n))일 때 를 모두 커버할 수 있는 방법입니다.
Solving ((A))((x)) ((=)) ((b)) -접근전략
((A))가 ((m)) < ((n))일 때, 주어진 방정식의 개수는 미지수의 개수보다 적습니다(해의 존재성 게시물을 확인해주시기 바랍니다). 그래서 이 방정식들을 만족시켜 줄 미지수들이 남아돕니다. 이렇게 어떤 값을 가져도 상관없는 친구들이 있습니다. ((A)) 내에서 dependent한 column들이 존재하는 경우에도 마찬가지입니다. 이들을 free variable이라고 합니다. 자유롭게 값을 assign 해줄 수 있는 것입니다.
그래서 free variable과 상관없이 방정식을 만족하는 해와, free variable들을 고려하는 해 이렇게 두 가지를 모두 구할 것입니다.
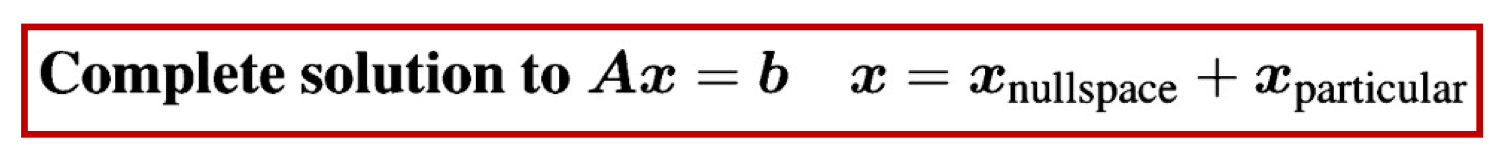
이게 바로 complete한 solution입니다.
free variable과 상관없이 방정식을 만족하는 해인 ((x_{particular}))와, free variable들을 고려하는, nullspace에서 차원이 무너질 때 같이 무너지는 벡터들을 표현하는 ((x_{nullspace}))를 모두 더해주어야 비로소 ((A))((x)) ((=)) ((b))의 완전한 해가 나오는 것입니다.
왜 이거 둘을 다 해라고 하는게 아니라 이들을 더해주는것인가 하면,

이렇게 더해주기 때문입니다.
Solving ((A))((x)) ((=)) ((b)) -풀이방법
우리는 행렬 ((A))를 rref 꼴로 분해하는 것부터 시작할 것입니다. 물론 우리는 해를 구할 것이므로, 이전 게시물의 "해를 바로 구하는 방법" 에서 보았던 Augmented Matrix를 또 이용하는 것입니다.
("해를 바로 구하는 방법" 은 아래 참조)
https://jaehoonstudy.tistory.com/12
Solving ((A))((x)) ((=)) ((b)) (When ((n)) x ((n))) - part 2
오늘은 지난 게시물에 이어서 ((A))((x)) ((=)) ((b))를 풀어야하는 상황에서 ((A))가 ((n)) x ((n)) 정방행렬일 때 이를 푸는 과정에 대해서 마저 다뤄보겠습니다. Part 1에서는 문제에 대한 접근 전략을 소
jaehoonstudy.tistory.com
자 그럼, 여느 때와 같이 예시와 시작해보겠습니다.
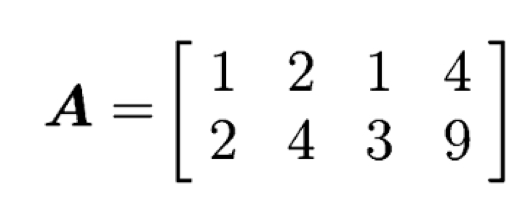
이게 우리의 ((A))라고 해봅시다. ((A))는 정방행렬이 아니고, ((m)) ((=)) ((2)), ((n)) ((=)) ((4))로, ((m)) < ((n))인 경우입니다.
항상 경우를 나누면 좋습니다. 그러면 우리가 공부했던 조건에 따라 해가 무조건 하나 이상 있을 것입니다.
우리는 ((A))((x)) ((=)) ((b))의 해를 구하는게 목표이기에, ((b))를 ((A)) 끝에 Augment 해줍니다(뒤에 붙여줍니다). 그 후 ((A))를 rref의 형태로 바꿔주도록 하겠습니다.
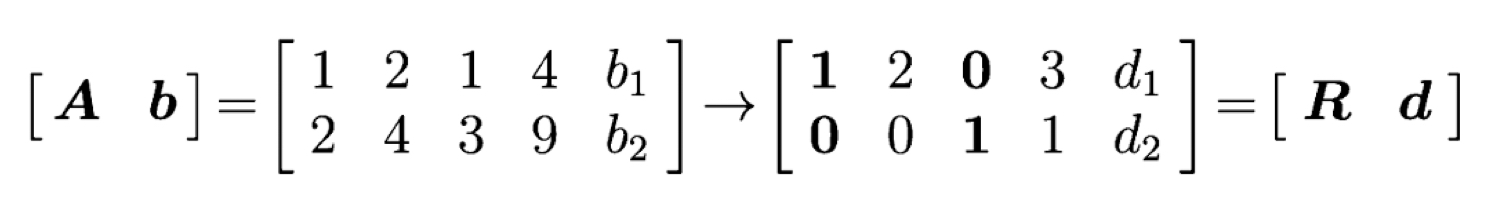
이런 모양으로 되겠죠. 참고로 pivot은 1행 맨 앞에 1과, 2행의 3번째 3입니다. 뒤의 ((d))들은 상수항 ((b))들에 연산을 취해준걸 대충 뭉뚱그려서 ((d))라고 표현한 것입니다. ((d))의 연산과정을 정확히 보면,
((\begin{bmatrix}
1 & 2 & 1 & 4 & b₁\\
2 & 4 & 3 & 9 & b₂
\end{bmatrix}))
((\begin{bmatrix}
1 & 2 & 1 & 4 & b\\
0 & 0 & 1 & 1 & b₂ -2b₁
\end{bmatrix}))
((\begin{bmatrix}
1 & 2 & 0 & 3 & b₁-b₂+2b₁\\
0 & 0 & 1 & 1 & b₂ -2b₁
\end{bmatrix}))
이런 식의 일련의 과정일 것입니다. 지금은 뒤의 ((b))들을 뭉뚱그려 ((d))들이라고 하겠습니다.
((x_{particular})) 를 구하는 법
첫 번째 solution을 구하기 위해서는 바로 dependent한 column들, free variable들을 일단 0으로 만들어주고 방정식을 계산하는 것입니다.
우리가 행렬을 rref로 분해하였을 때 identity matrix가 나오는 부분은 바로 행렬의 independent한, 독립적인 column들입니다. 얘네는 살리고 가고, 일단은 free variable과 상관없이 방정식을 만족하는 ((x_{particular}))을 구하는 것이기에 0으로 놓고 푸는 것입니다.
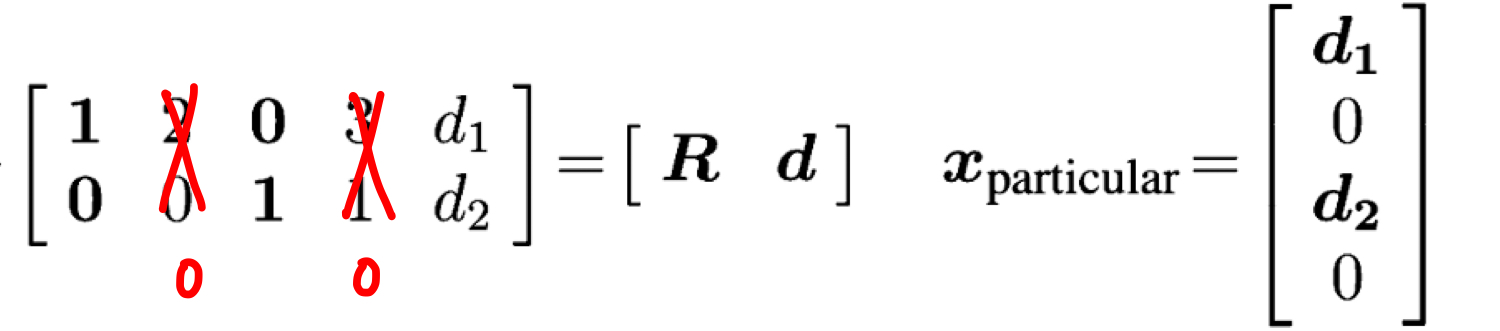
이게 무슨 뜻이냐하면, 지금 행렬 계산을 보시면 앞에 행렬이 2x4, 그리고 ((b))가 2x1이기에 ((x))는 4x1의 형태를 가집니다. ((x))의 성분이 4개니까 ((x))가 ((x₁)) 부터 ((x₄)) 까지 있다고 하면, 미지수가 4개이고, 바로 위의 방정식 그림은 아래의 식과 같이 나타낼 수 있습니다.
((x_{1})) + 2((x_{2})) + 0((x_{3})) + 3((x_{4})) = ((d_{1}))
0((x_{1})) + 0((x_{2})) + ((x_{3})) + ((x_{4})) = ((d_{2}))
라는 뜻입니다. 이제 free variable을 무시하기 위해, ((x_{2})) = 0, ((x_{4})) = 0 이라고 가정해보겠습니다.
그렇게 되면 ((x_{1})) = ((d_{1}))이 되며, ((x_{3})) = ((d_{2}))가 됩니다.
이게 바로 free variable을 고려하지 않은 ((x_{particular}))가 되는 것입니다.
((x_{nullspace}))를 구하는 방법
두 번째 solution을 구하기 위해서는 rref의 생김새를 다시 한 번 볼 필요가 있습니다. 지금 행렬에는 4개의 column이 있습니다.
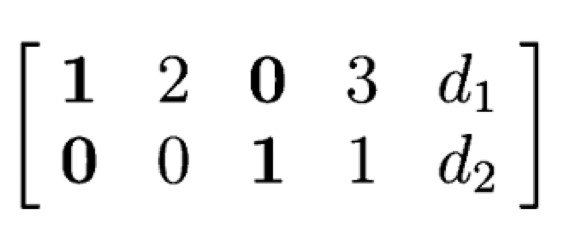
그런데 4개의 column이 있으면 이를 최대로 활용하는 full rank인 4개의 independent한 column이 있는게 아니라, independent한 column은 identity의 형태로 나타나는 2개밖에 없고, 나머지 2개는 dependent한 column들입니다.
이전에 부분공간을 다룬 게시물에서도 나와있지만, 이런 경우에는 ((r))개의 independent한 column이 있고, Nullspace는 ((n)) - ((r))의 차원을 가집니다. 당연한것이, dependent한 column들은 제가 계속 강조드렸듯이 '차원이 무너지기' 때문에 nullspace로 가는 것입니다. 아주 직관적으로는, 열이 4개니까 4차원이 되어야하는데 지금 2차원 밖에 없으니, 나머지 2개는 0으로 갔다(nullspace로) 라고 생각하시면 매우 쉽습니다. 그러면 2개의 해의 basis가 또 있을 것입니다.
우리에게는 free variable이 2개 있습니다. 이 free variable들에게 임의로 값을 할당해줄 건데, 여러 개의 free variable 중에 1개만 1로 놓고 나머지는 0으로 놓는 방식입니다.
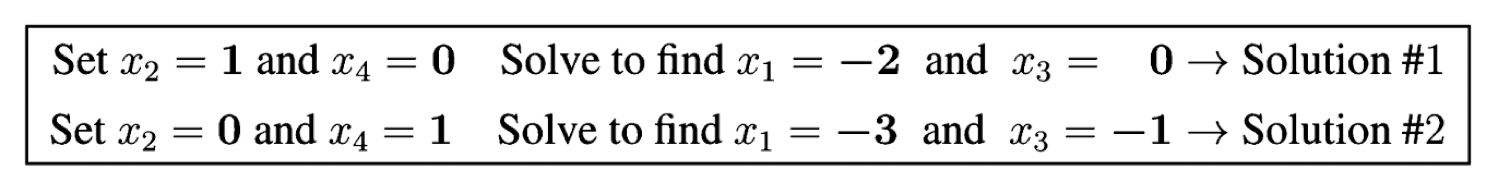
((x_{2}))를 1로 놓고 나머지는 전부 0, (지금 우리는 2개니까 자동으로 나머지 하나인 ((x_{4}))가 0이 됩니다)
((x_{4}))를 1로 놓고 나머지는 전부 0으로 놓는 것입니다.
그리고 선형방정식계를 푼다면,
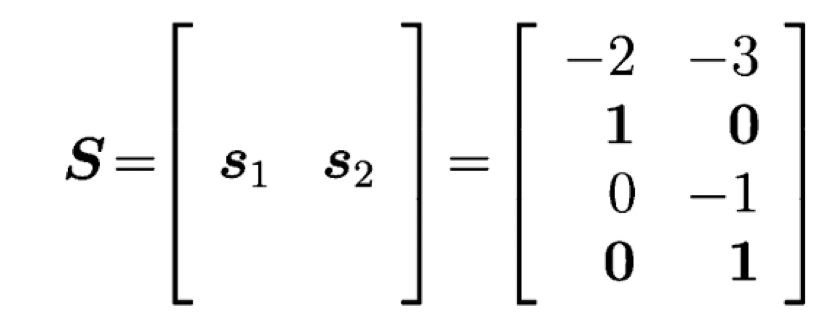
Nullspace의 solution 2개는 각각 이런 형태를 가질 것입니다. 바로 independent한 column들의 combination의 형태로 dependent한 column들이 나오는 것입니다.
결론

바로 이게 ((A))((x)) ((=)) ((b))의 완전한 해인 것입니다. 앞에 ((c))들은 상수로, 우리가 지금 앞에 두 개를 구한 것은 nullspace의 basis이기 때문에, basis를 배수해주고 서로 더하는 것도 다 해가 됩니다(이전의 해의 존재성에서 모든 초록색 점들이 0으로 무너지는 것을 다시 상상해볼 수 있습니다). 그래서 앞의 nullspace의 basis 간의 linear combination과, free variable 없이 그대로 구한 ((x_{particular}))을 더해준 것이 바로 완전한 해인 것입니다.
'선형대수' 카테고리의 다른 글
| 부분공간에 벡터 투영시키기(Projection onto Subspaces) (0) | 2024.02.16 |
|---|---|
| 직교성(Orthogonality)과 부분공간(Subspaces) (1) | 2024.01.31 |
| 선형연립방정식의 해의 존재성 (1) | 2024.01.30 |
| Gauss-Jordan Elimination(가우스-조던 소거법) & RREF (1) | 2024.01.29 |
| Four Fundamental Subspaces(4개의 주요 부분공간) (0) | 2024.01.28 |
저번 게시물에서 해의 존재성에 대해 자세히 다뤘었습니다. 이번에는 드디어 해가 존재할 때, 이를 어떻게 푸는지 알아보도록 하겠습니다. 이전에는 ((A))가 ((m)) = ((n))이고 dependent한 column이 없는 특수한 경우만 다뤘었다면, 이제는 이를 일반화 시켜서 해가 존재할 때, ((A)) 내에 dependent한 column들이 있을 때도, ((A))가 ((m)) = ((n))인 정방행렬(square matrix)이 아닐 때도 통하는 방법에 대해서 다루는 것입니다.
((A))((x)) ((=)) ((b))의 complete solution을 구하는 방법
저번 게시물인 해의 존재성에 대한 게시물을 보시지 않으셨다면, 이를 반드시 보고 오시는 것을 추천드립니다.
https://jaehoonstudy.tistory.com/18
선형연립방정식의 해의 존재성
오늘은, 우리가 푸는 문제인, ((A))((x)) ((=)) ((b)) 를 풀기 전 확인해야하는 해의 존재성에 대해서 알아보도록 하겠습니다. 해가 유일할 때, 없을 때, 무한할 때와 그에 따른 ((A))의 모양과 함꼐 연관
jaehoonstudy.tistory.com
그리고 rref에 대해서도 한 번 다시 보시고 오는 것을 추천드립니다.
https://jaehoonstudy.tistory.com/17
Gauss-Jordan Elimination(가우스-조던 소거법) & RREF
오늘은 이전 게시물에서 다루었던 부분공간들을 발견할 수 있는, 그리고 이후 문제 해결에서 도움이 되는 가우스-조던 소거법과, rref(기약 행사다리꼴)에 대해서 알아보도록 하겠습니다. Gauss-Jor
jaehoonstudy.tistory.com
지금 다루는 경우가 어떤 경우인가?
일단 지금 다루려는 경우, 지금 아래에 서술할 방법론이 어떤 경우에 쓰이는 방법인지 명확하게 인지하고 넘어갈 필요가 있습니다.
선형방정식계에서 매우 크게 경우의 수를 분류하면, 해가 존재할 수도 있고 존재하지 않을 수도 있습니다. 해의 존재성 게시물에서 보셨겠지만, 경우는 다음과 같습니다.

A가 ((m)) > ((n))일 때는, 매우 드물게 ((b))가 ((A))의 column space 내에 존재하는 경우에 해가 있습니다.
지금 중점적으로 다루려는 경우는 해가 존재할 때, 즉 ((A))가 정방행렬인데 dependent column이 있을 때, 그리고 ((A))가 ((m)) < ((n))일 때 를 모두 커버할 수 있는 방법입니다.
Solving ((A))((x)) ((=)) ((b)) -접근전략
((A))가 ((m)) < ((n))일 때, 주어진 방정식의 개수는 미지수의 개수보다 적습니다(해의 존재성 게시물을 확인해주시기 바랍니다). 그래서 이 방정식들을 만족시켜 줄 미지수들이 남아돕니다. 이렇게 어떤 값을 가져도 상관없는 친구들이 있습니다. ((A)) 내에서 dependent한 column들이 존재하는 경우에도 마찬가지입니다. 이들을 free variable이라고 합니다. 자유롭게 값을 assign 해줄 수 있는 것입니다.
그래서 free variable과 상관없이 방정식을 만족하는 해와, free variable들을 고려하는 해 이렇게 두 가지를 모두 구할 것입니다.
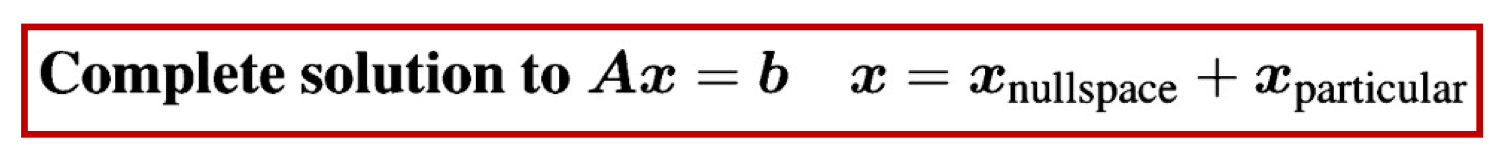
이게 바로 complete한 solution입니다.
free variable과 상관없이 방정식을 만족하는 해인 ((x_{particular}))와, free variable들을 고려하는, nullspace에서 차원이 무너질 때 같이 무너지는 벡터들을 표현하는 ((x_{nullspace}))를 모두 더해주어야 비로소 ((A))((x)) ((=)) ((b))의 완전한 해가 나오는 것입니다.
왜 이거 둘을 다 해라고 하는게 아니라 이들을 더해주는것인가 하면,

이렇게 더해주기 때문입니다.
Solving ((A))((x)) ((=)) ((b)) -풀이방법
우리는 행렬 ((A))를 rref 꼴로 분해하는 것부터 시작할 것입니다. 물론 우리는 해를 구할 것이므로, 이전 게시물의 "해를 바로 구하는 방법" 에서 보았던 Augmented Matrix를 또 이용하는 것입니다.
("해를 바로 구하는 방법" 은 아래 참조)
https://jaehoonstudy.tistory.com/12
Solving ((A))((x)) ((=)) ((b)) (When ((n)) x ((n))) - part 2
오늘은 지난 게시물에 이어서 ((A))((x)) ((=)) ((b))를 풀어야하는 상황에서 ((A))가 ((n)) x ((n)) 정방행렬일 때 이를 푸는 과정에 대해서 마저 다뤄보겠습니다. Part 1에서는 문제에 대한 접근 전략을 소
jaehoonstudy.tistory.com
자 그럼, 여느 때와 같이 예시와 시작해보겠습니다.
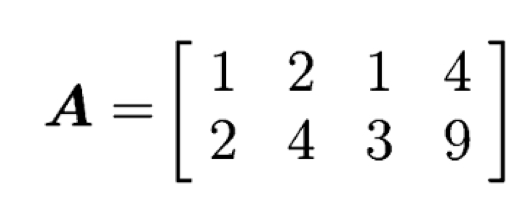
이게 우리의 ((A))라고 해봅시다. ((A))는 정방행렬이 아니고, ((m)) ((=)) ((2)), ((n)) ((=)) ((4))로, ((m)) < ((n))인 경우입니다.
항상 경우를 나누면 좋습니다. 그러면 우리가 공부했던 조건에 따라 해가 무조건 하나 이상 있을 것입니다.
우리는 ((A))((x)) ((=)) ((b))의 해를 구하는게 목표이기에, ((b))를 ((A)) 끝에 Augment 해줍니다(뒤에 붙여줍니다). 그 후 ((A))를 rref의 형태로 바꿔주도록 하겠습니다.
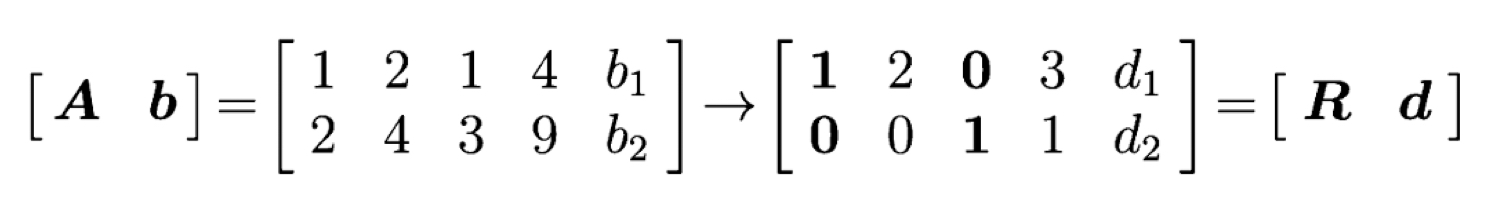
이런 모양으로 되겠죠. 참고로 pivot은 1행 맨 앞에 1과, 2행의 3번째 3입니다. 뒤의 ((d))들은 상수항 ((b))들에 연산을 취해준걸 대충 뭉뚱그려서 ((d))라고 표현한 것입니다. ((d))의 연산과정을 정확히 보면,
((\begin{bmatrix}
1 & 2 & 1 & 4 & b₁\\
2 & 4 & 3 & 9 & b₂
\end{bmatrix}))
((\begin{bmatrix}
1 & 2 & 1 & 4 & b\\
0 & 0 & 1 & 1 & b₂ -2b₁
\end{bmatrix}))
((\begin{bmatrix}
1 & 2 & 0 & 3 & b₁-b₂+2b₁\\
0 & 0 & 1 & 1 & b₂ -2b₁
\end{bmatrix}))
이런 식의 일련의 과정일 것입니다. 지금은 뒤의 ((b))들을 뭉뚱그려 ((d))들이라고 하겠습니다.
((x_{particular})) 를 구하는 법
첫 번째 solution을 구하기 위해서는 바로 dependent한 column들, free variable들을 일단 0으로 만들어주고 방정식을 계산하는 것입니다.
우리가 행렬을 rref로 분해하였을 때 identity matrix가 나오는 부분은 바로 행렬의 independent한, 독립적인 column들입니다. 얘네는 살리고 가고, 일단은 free variable과 상관없이 방정식을 만족하는 ((x_{particular}))을 구하는 것이기에 0으로 놓고 푸는 것입니다.
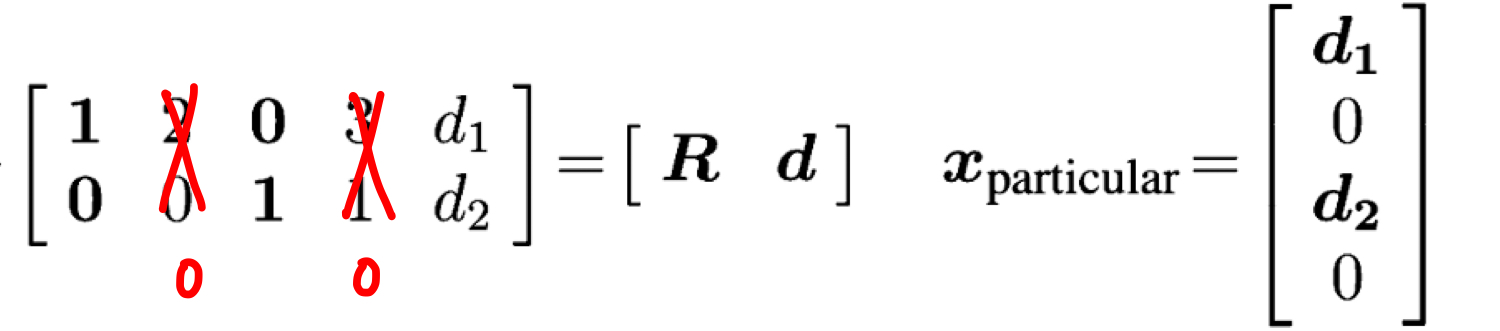
이게 무슨 뜻이냐하면, 지금 행렬 계산을 보시면 앞에 행렬이 2x4, 그리고 ((b))가 2x1이기에 ((x))는 4x1의 형태를 가집니다. ((x))의 성분이 4개니까 ((x))가 ((x₁)) 부터 ((x₄)) 까지 있다고 하면, 미지수가 4개이고, 바로 위의 방정식 그림은 아래의 식과 같이 나타낼 수 있습니다.
((x_{1})) + 2((x_{2})) + 0((x_{3})) + 3((x_{4})) = ((d_{1}))
0((x_{1})) + 0((x_{2})) + ((x_{3})) + ((x_{4})) = ((d_{2}))
라는 뜻입니다. 이제 free variable을 무시하기 위해, ((x_{2})) = 0, ((x_{4})) = 0 이라고 가정해보겠습니다.
그렇게 되면 ((x_{1})) = ((d_{1}))이 되며, ((x_{3})) = ((d_{2}))가 됩니다.
이게 바로 free variable을 고려하지 않은 ((x_{particular}))가 되는 것입니다.
((x_{nullspace}))를 구하는 방법
두 번째 solution을 구하기 위해서는 rref의 생김새를 다시 한 번 볼 필요가 있습니다. 지금 행렬에는 4개의 column이 있습니다.
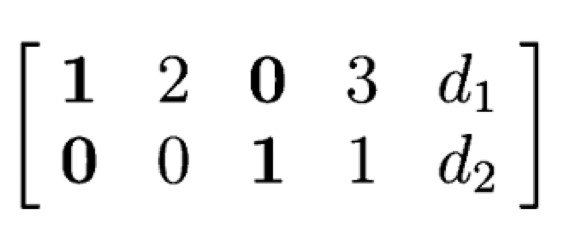
그런데 4개의 column이 있으면 이를 최대로 활용하는 full rank인 4개의 independent한 column이 있는게 아니라, independent한 column은 identity의 형태로 나타나는 2개밖에 없고, 나머지 2개는 dependent한 column들입니다.
이전에 부분공간을 다룬 게시물에서도 나와있지만, 이런 경우에는 ((r))개의 independent한 column이 있고, Nullspace는 ((n)) - ((r))의 차원을 가집니다. 당연한것이, dependent한 column들은 제가 계속 강조드렸듯이 '차원이 무너지기' 때문에 nullspace로 가는 것입니다. 아주 직관적으로는, 열이 4개니까 4차원이 되어야하는데 지금 2차원 밖에 없으니, 나머지 2개는 0으로 갔다(nullspace로) 라고 생각하시면 매우 쉽습니다. 그러면 2개의 해의 basis가 또 있을 것입니다.
우리에게는 free variable이 2개 있습니다. 이 free variable들에게 임의로 값을 할당해줄 건데, 여러 개의 free variable 중에 1개만 1로 놓고 나머지는 0으로 놓는 방식입니다.
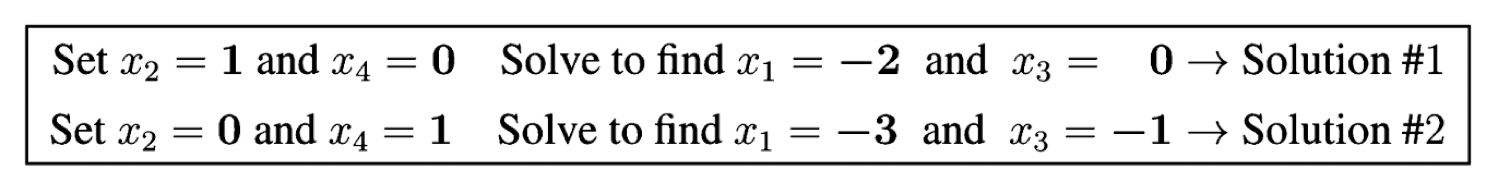
((x_{2}))를 1로 놓고 나머지는 전부 0, (지금 우리는 2개니까 자동으로 나머지 하나인 ((x_{4}))가 0이 됩니다)
((x_{4}))를 1로 놓고 나머지는 전부 0으로 놓는 것입니다.
그리고 선형방정식계를 푼다면,

Nullspace의 solution 2개는 각각 이런 형태를 가질 것입니다. 바로 independent한 column들의 combination의 형태로 dependent한 column들이 나오는 것입니다.
결론

바로 이게 ((A))((x)) ((=)) ((b))의 완전한 해인 것입니다. 앞에 ((c))들은 상수로, 우리가 지금 앞에 두 개를 구한 것은 nullspace의 basis이기 때문에, basis를 배수해주고 서로 더하는 것도 다 해가 됩니다(이전의 해의 존재성에서 모든 초록색 점들이 0으로 무너지는 것을 다시 상상해볼 수 있습니다). 그래서 앞의 nullspace의 basis 간의 linear combination과, free variable 없이 그대로 구한 ((x_{particular}))을 더해준 것이 바로 완전한 해인 것입니다.
'선형대수' 카테고리의 다른 글
| 부분공간에 벡터 투영시키기(Projection onto Subspaces) (0) | 2024.02.16 |
|---|---|
| 직교성(Orthogonality)과 부분공간(Subspaces) (1) | 2024.01.31 |
| 선형연립방정식의 해의 존재성 (1) | 2024.01.30 |
| Gauss-Jordan Elimination(가우스-조던 소거법) & RREF (1) | 2024.01.29 |
| Four Fundamental Subspaces(4개의 주요 부분공간) (0) | 2024.01.28 |
