오늘은 inverse matrix에 대해 다뤄보려고 합니다.
Matrix는 Linear transformation이고, 일종의 함수입니다. input이 들어오면 이렇게저렇게 뭔가를 바꿔서 output이 나오기 때문입니다. 그렇다면 어떤 함수의 역함수도 있을 수 있을 것입니다. 그것이 행렬의 개념으로 들어온게 바로 역행렬입니다. 결국 직관적으로 이해하자면 행렬은 변환이었으니, '역변환' 정도가 되지 않을까 싶습니다.
Inverse의 역할
선형대수학의 목적은 선형방정식들을 잘 표현하고, 그들의 해를 구하는 것입니다. 어떤 Matrix의 inverse를 알 수 있다면, 우리는 그 선형방정식들의 해를 구할 수 있습니다.
((A))((x)) = ((b))
형태의 식이 있을 때, 이것이 의미하는 바는 A의 column들을 어떻게 조합하면(((x))) ((b))가 나올까? 라는 것입니다. 그 '어떻게' 가 바로 이 선형방정식들의 해인 것입니다. 그런데 행렬은 선형변환이므로, 관점을 다르게 하면 어떤 벡터 ((x))에 우리가 변환 A를 가했더니 벡터 ((b))가 결과로 나왔다고도 볼 수 있습니다. 그렇다면 우리는 결과 ((b))를 알고 있으니, 벡터 ((b))에다가 변환 ((A))의 역변환인 ((A^{-1}))를 가한다면 다시 원상태인 벡터 ((x))로 되돌릴 수 있을 것입니다. 이것이 역행렬의 의의입니다. 결국 선형방정식의 해는,
((x)) = ((A^{-1}))((b))
로 나타낼 수 있습니다.
Inverse matrix의 정의
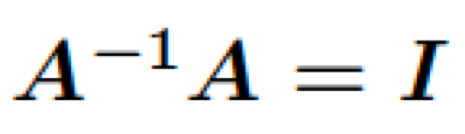
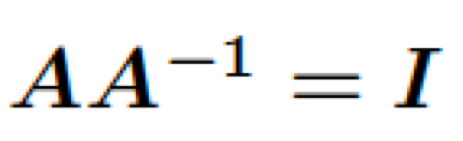
다음과 같은 성질을 만족하는 ((A^{-1}))을 역행렬이라 합니다.
Inverse matrix 구하는 법

역행렬은 위와 같이 구합니다.
이후에도 이야기가 나오겠지만, matrix의 크기가 커지면 커질 수록 inverse를 구할 때 computational cost가 많이 들어갑니다. 그리고 우리가 직접 계산할 때도 역행렬을 일일이 다 계산하기란 매우 어려운 일입니다. 그래서 다양한 방법들로 행렬에 변화를 가해 조금 더 쉬운 형태의 행렬꼴로 만드는 경우들이 대부분입니다.
Determinant와 Inverse
위의 식을 보면 바로 알 수 있듯이, ((ad)) - ((bc))가 0이 되어버리면 분모가 0인 수가 나와버리기에 불가능합니다. 그렇기 때문에 ((det(A)))가 0일 때, 공간이 찌부러질 때, 역행렬은 존재하지 않습니다. 지난 게시물에서 determinant를 다룰 때, 공간이 찌부러지는 변환은 다시 되돌릴 수 없다고 이야기했는데, 바로 이것입니다.
A가 inverse가 없다는 것은:
- determinant가 0이다.
- dependent row가 있다.
- dependent column이 있다.
- singular matrix이다.
와 동치입니다. 그리고 inverse가 없을 때 그 행렬을 non-invertible하다고 하고, inverse가 있을 때는 invertible 하다고 합니다.
Inverse의 특징들
- 어떤 행렬이 Invertible할 경우 Row와 Column이 모두 independent 합니다.
- 행렬의 주 대각선(main diagonal)에 0이 없습니다(((ad))-((bc))가 0이 아닙니다).
- ((AB))의 inverse는 ((B^{-1}))((A^{-1}))입니다.
- invertible하다는 뜻은 ((A))((x)) = ((b))의 유일한 해가 ((x)) = ((A^{-1}))((b))라는 뜻입니다.
- ((A^{-1}))를 계산하는 것은 computationally inefficient 합니다.
'선형대수' 카테고리의 다른 글
| Solving ((A))((x)) ((=)) ((b)) (When ((n)) x ((n))) - part 2 (2) | 2024.01.26 |
|---|---|
| Solving ((A))((x)) ((=)) ((b)) (When ((n)) x ((n))) - part 1 (1) | 2024.01.22 |
| 행렬식(Determinant) (0) | 2024.01.18 |
| CR Factorization (0) | 2024.01.18 |
| 행렬의 곱셈(Matrix-Matrix Multiplication) (0) | 2024.01.17 |
오늘은 inverse matrix에 대해 다뤄보려고 합니다.
Matrix는 Linear transformation이고, 일종의 함수입니다. input이 들어오면 이렇게저렇게 뭔가를 바꿔서 output이 나오기 때문입니다. 그렇다면 어떤 함수의 역함수도 있을 수 있을 것입니다. 그것이 행렬의 개념으로 들어온게 바로 역행렬입니다. 결국 직관적으로 이해하자면 행렬은 변환이었으니, '역변환' 정도가 되지 않을까 싶습니다.
Inverse의 역할
선형대수학의 목적은 선형방정식들을 잘 표현하고, 그들의 해를 구하는 것입니다. 어떤 Matrix의 inverse를 알 수 있다면, 우리는 그 선형방정식들의 해를 구할 수 있습니다.
((A))((x)) = ((b))
형태의 식이 있을 때, 이것이 의미하는 바는 A의 column들을 어떻게 조합하면(((x))) ((b))가 나올까? 라는 것입니다. 그 '어떻게' 가 바로 이 선형방정식들의 해인 것입니다. 그런데 행렬은 선형변환이므로, 관점을 다르게 하면 어떤 벡터 ((x))에 우리가 변환 A를 가했더니 벡터 ((b))가 결과로 나왔다고도 볼 수 있습니다. 그렇다면 우리는 결과 ((b))를 알고 있으니, 벡터 ((b))에다가 변환 ((A))의 역변환인 ((A^{-1}))를 가한다면 다시 원상태인 벡터 ((x))로 되돌릴 수 있을 것입니다. 이것이 역행렬의 의의입니다. 결국 선형방정식의 해는,
((x)) = ((A^{-1}))((b))
로 나타낼 수 있습니다.
Inverse matrix의 정의
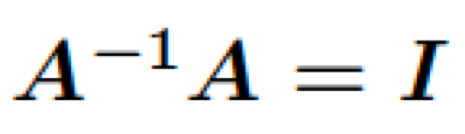
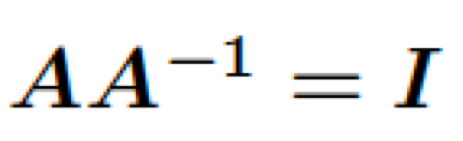
다음과 같은 성질을 만족하는 ((A^{-1}))을 역행렬이라 합니다.
Inverse matrix 구하는 법

역행렬은 위와 같이 구합니다.
이후에도 이야기가 나오겠지만, matrix의 크기가 커지면 커질 수록 inverse를 구할 때 computational cost가 많이 들어갑니다. 그리고 우리가 직접 계산할 때도 역행렬을 일일이 다 계산하기란 매우 어려운 일입니다. 그래서 다양한 방법들로 행렬에 변화를 가해 조금 더 쉬운 형태의 행렬꼴로 만드는 경우들이 대부분입니다.
Determinant와 Inverse
위의 식을 보면 바로 알 수 있듯이, ((ad)) - ((bc))가 0이 되어버리면 분모가 0인 수가 나와버리기에 불가능합니다. 그렇기 때문에 ((det(A)))가 0일 때, 공간이 찌부러질 때, 역행렬은 존재하지 않습니다. 지난 게시물에서 determinant를 다룰 때, 공간이 찌부러지는 변환은 다시 되돌릴 수 없다고 이야기했는데, 바로 이것입니다.
A가 inverse가 없다는 것은:
- determinant가 0이다.
- dependent row가 있다.
- dependent column이 있다.
- singular matrix이다.
와 동치입니다. 그리고 inverse가 없을 때 그 행렬을 non-invertible하다고 하고, inverse가 있을 때는 invertible 하다고 합니다.
Inverse의 특징들
- 어떤 행렬이 Invertible할 경우 Row와 Column이 모두 independent 합니다.
- 행렬의 주 대각선(main diagonal)에 0이 없습니다(((ad))-((bc))가 0이 아닙니다).
- ((AB))의 inverse는 ((B^{-1}))((A^{-1}))입니다.
- invertible하다는 뜻은 ((A))((x)) = ((b))의 유일한 해가 ((x)) = ((A^{-1}))((b))라는 뜻입니다.
- ((A^{-1}))를 계산하는 것은 computationally inefficient 합니다.
'선형대수' 카테고리의 다른 글
| Solving ((A))((x)) ((=)) ((b)) (When ((n)) x ((n))) - part 2 (2) | 2024.01.26 |
|---|---|
| Solving ((A))((x)) ((=)) ((b)) (When ((n)) x ((n))) - part 1 (1) | 2024.01.22 |
| 행렬식(Determinant) (0) | 2024.01.18 |
| CR Factorization (0) | 2024.01.18 |
| 행렬의 곱셈(Matrix-Matrix Multiplication) (0) | 2024.01.17 |
