오늘은 CR factorization, 즉, Column-Row factorization에 대해서 다뤄볼 예정입니다.
CR Factorization은 무엇인가?
CR factorization은 Column-Row factorization의 약자입니다.
이 CR factorization으로 우리는 Matrix의 Rank를 알 수 있습니다.
또한, 이전에 언급했던 모든 행렬의 Column rank와 row rank가 같은지에 대한 증명이기도 합니다.
왜 CR factorization이냐 하면, 일단 factorization이 분해라는 뜻입니다. 그러니까 직역하면 CR 분해입니다. 지금부터 행렬 A를 행렬 C와 행렬 R 간의 곱으로 분해해 볼 것입니다.
CR factorization 하는 방법
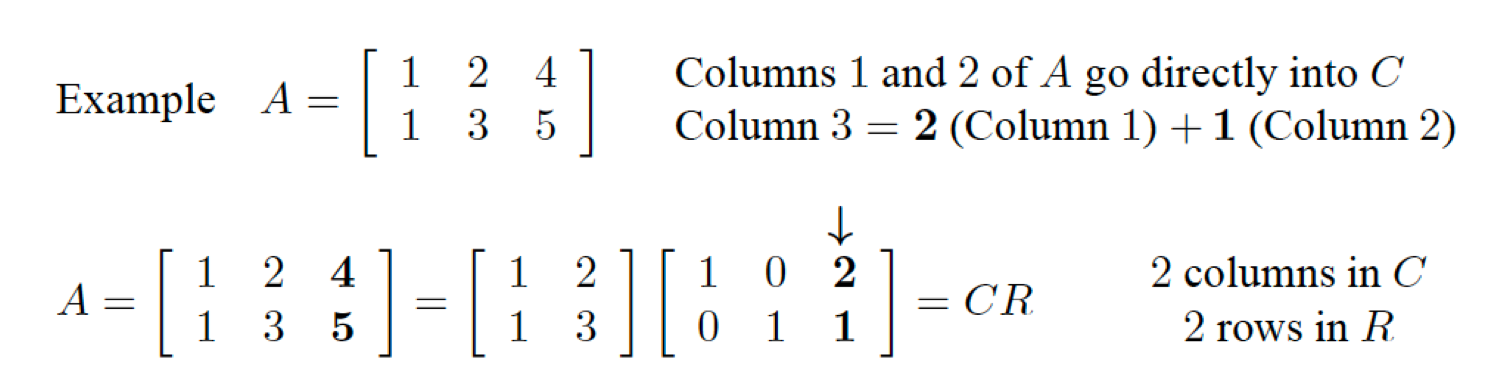
현재 A라는 행렬 ((\begin{bmatrix}
1 & 2 & 4\\
1 & 3 & 5
\end{bmatrix})) 가 있습니다. 먼저 이 행렬을 잘 들여다보시면, dependent column이 있다는 것을 눈치채실 수 있을 것입니다. Column 1을 2배하고, column 2랑 더해주면 column 3이 나오는게 보이시나요?
((2\begin{bmatrix}
1\\
1
\end{bmatrix})) + ((\begin{bmatrix}
2\\
3
\end{bmatrix})) = ((\begin{bmatrix}
4\\
5
\end{bmatrix}))
1. 먼저 independent column들로 matrix C를 구성합니다.
이 경우에는 ((2\begin{bmatrix}
1\\
1
\end{bmatrix})) 와 ((\begin{bmatrix}
2\\
3
\end{bmatrix}))를 앞에 써주면 되겠습니다.
2. Matrix R의 경우 우선, 독립적인 column들이 있던 위치에 그대로 identity matrix로 채웁니다.
이 경우에는 matrix A에서 첫 번째와 두 번째가 independent column이니 R의 첫 번째, 두 번째 column들을 identity matrix로 만들어줍니다.
Identity matrix란?
Identity Matrix는 항등행렬로, 주대각선의 원소가 모두 1이며 나머지는 0인 행렬을 의미합니다.

만약 행렬 A와 곱해진다면 행렬 A가 그대로 나오는, 숫자 1을 곱하는 것과 같은 느낌입니다.
3. Linear combination의 계수들을 dependent column의 자리에 그대로 써주며 R을 완성합니다.
((2\begin{bmatrix}
1\\
1
\end{bmatrix})) + ((\begin{bmatrix}
2\\
3
\end{bmatrix})) = ((\begin{bmatrix}
4\\
5
\end{bmatrix}))
지금 행렬 A는 첫 번째 column을 2배, 두 번째 column을 1배하여 마지막 column이 구성되는 구조이므로, 각각의 Linear combination의 계수는 2,1입니다. 이를 ((\begin{bmatrix}
2\\
1
\end{bmatrix})) 이렇게 구성하여 남은 R의 자리를 채워줍니다.
이렇게 C는,
A의 첫 r개의 independent column들이 뭐가 있는지 직접적으로 보여줍니다.
R은,
A의 independent column들이 어디에 있는지 identity matrix로 보여줍니다.
보시면,
A,C,R 모두 column rank가 2입니다.
A,C,R 모두 row rank도 2입니다.
Column rank = Row rank 증명
Now, each row of A is given by a linear combination of the r rows of R. Therefore, the rows of R form a spanning set of the row space of A. By the Steinitz exchange lemma, the row rank of A cannot exceed r. This proves that the row rank of A is less than or eqaul to the column rank of A.
This result can be applied to any matrix, so apply the result to the transpose of A. Since the row rank of the transpose of A is the column rank of A and the column rank of the transpose of A is the row rank of A, this establishes the reverse inequality, and we obtain the equality of the row rank and the column rank of A.
'Linear Algebra' 카테고리의 다른 글
| Inverse Matrix(역행렬) (0) | 2024.01.18 |
|---|---|
| 행렬식(Determinant) (0) | 2024.01.18 |
| 행렬의 곱셈(Matrix-Matrix Multiplication) (0) | 2024.01.17 |
| 행렬(Matrix)의 Rank (0) | 2024.01.16 |
| 행렬(Matrix) - Column space & Row space (0) | 2024.01.16 |
