이전 포스트에서는 강화학습이란 무엇인가? 그리고 나오는 key concept들에 대해서 알아보았다. 아직 기본 개념들에 익숙하지 않다면 꼭 이전 게시물을 보고 오는 것을 추천한다. 그럼 이어서 강화학습에 대해 더욱 다루어보도록 하자.
MDP (Markov Decision Process)
강화학습에서는 대부분의 과제를 MDP로 모델링하여 해결한다. 그래야지만 우리가 이전까지 다루었던 state, action, reward, 그리고 transition probability를 써먹을 수가 있다.
Markov Property
MDP의 모든 state는 markov 성질을 만족한다. 약간 MDP가 가지고 있는 inductive bias 같은 거다.
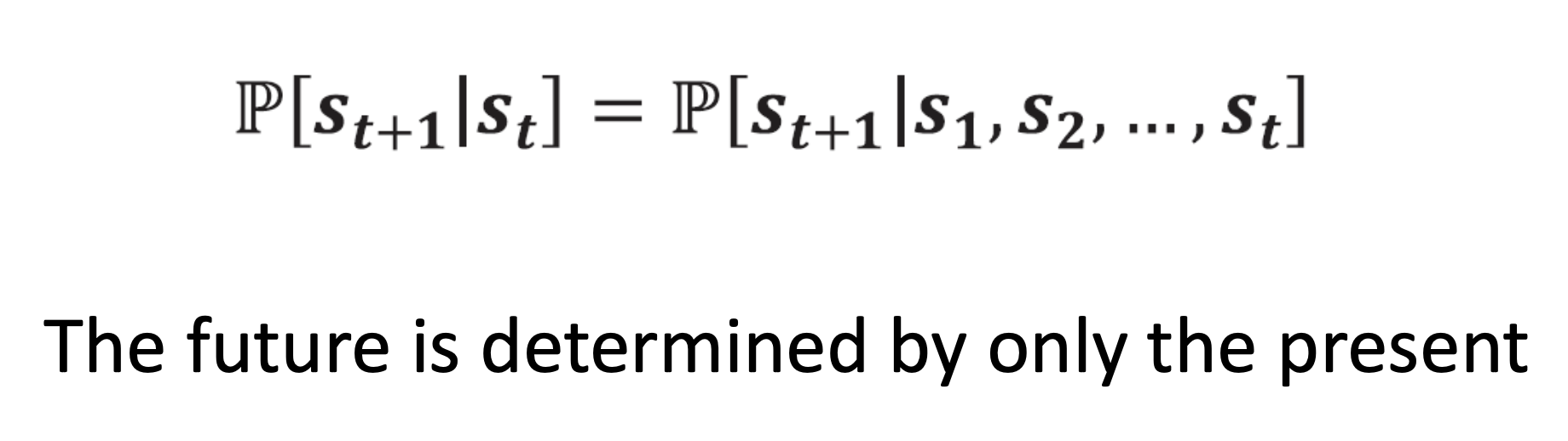
이건 무슨 뜻이냐면, 뒤에 조건부 확률이 있는데, st만 조건으로 준거랑 s1 부터 st까지 전부 조건으로 준거랑 아무 차이가 없다는 뜻이다. 즉, 과거의 정보를 다 때려넣어도 그냥 현재의 정보 하나만 준거랑 다음 state에 대해서 아무 차이가 없다는 뜻이다.
즉, future와 past history는 conditionally independent, 독립적으로 치겠다는 것이다.
Why is Markov Assumption popular?
- Markov property를 만족하는 policy는 optimal하게 될 수 있기 때문이다.
- 항상 만족시킬 수 있다. (과거에 영향 받지 않기 때문에)
MDP elements
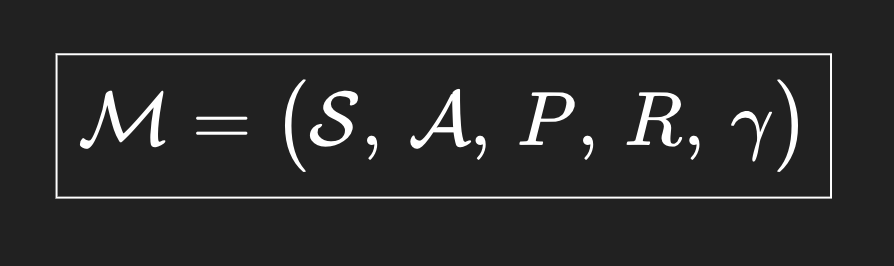
각각의 정의는, 여태까지 우리가 봤던 것 그대로이다.

Deepmind의 강화학습의 대가, David Silver의 MDP의 한 예시를 보자.

Class 1에 출석한다, Facebook을 한다, Pub에 간다, Sleep 과 같은 다양한 state와 action들이 있고, 그에 따른 transition probability도 있으며 (0.2, 0.4 등등) 각각에 따른 보상도 빨간색 R로 적혀있다.
Bellman Equations
간단하게 생각하자 간단하게. 이건 뭐냐면,
Value function을 지금 당장의 보상 + 미래의 보상 으로 분리하여 서술하는 equation들
을 말한다.

식이 이리저리 나오긴 하나, 어떻게 보면 당연한 것인데, 현재 state s에서의 최종 return은 지금 당장 나오는 보상 + 미래에 나오는 보상 이렇게 분해할 수 있기 때문이다. 어차피 다 더하면 최종 리턴값이 되니까.
Q-value도 마찬가지이다. 전부 보면 지금 당장의 한 스텝 보상 + 감마가 적용된 미래의 보상으로 분해되어있다.
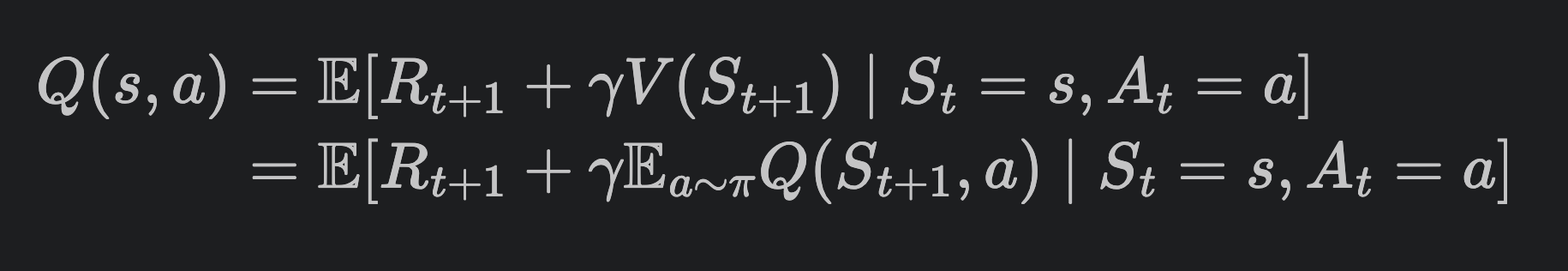
Bellman Expectation Equations
얘도 간단하게 생각하자. 간단하게; 이건 뭐냐면,
현재 state의 value function을 다음 state의 value function을 통해 표현하는 것이다.
일단 이걸 왜 하냐면, 무한대인 infinte-horizon 문제를 간단하게 "한 스텝 + 다음 스텝" 으로 나눠주기 때문이다.
여태까지 value function 보면서 '아니, 모든 future value를 어떻게 계산하지? 경우의 수가 어떻게 될 줄 알고?' 라는 생각은 안 들었는가? 얘를 이용해서 한 스텝씩 분해해나가면, 비로소 우리가 계산할 수 있는 형태가 되는 것이다.
일단, value function에는 state-value function과 action-value function이 있었다. 얘네 둘 다, 상대방을 이용해서 다시 쓸 수 있다.
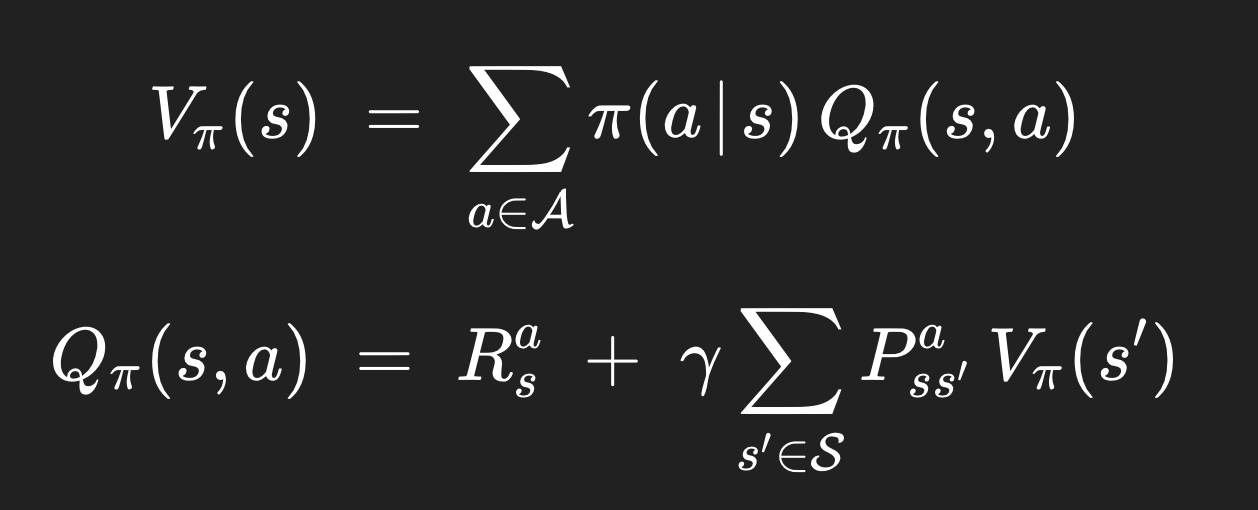
state-value: 특정 action이 일어날 확률 x 그 action에 대한 value , 그리고 모든 action들에 대해 sum해버리는 형태로,
action-value: 당장 그 action을 했을 때 나오는 reward + 미래의 reward (특정 다음 상태로 전이될 확률 x 특정 다음 상태의 가치, 그리고 모든 다음 상태를 고려하도록 sum해버리는)
이렇게 해석하는 것이다. 근데 여기서 보면 밑의 Q를 이용해서 첫 번째 V 식의 Q를 대체할 수 있다. 그리고 밑의 Q 식 같은 경우에는, 뒤에 V(s')가 있는데, V는 Q를 이용해서 다시 쓸 수 있었다 (첫 식을 봐라) .
그렇게 하면 다음과 같이 나온다.

이렇게 우리는 현재 state에서의 value를, 지금의 reward와 다음 state의 value function의 합으로 표현할 수 있다.
이게 왜 중요하냐면, 다음 state의 value function은 또 위의 식처럼 분해해버리면 되기 때문에, infinte한 문제를 recursive 하게, 하나하나 계산가능한 영역으로 끌어들였다는 점이 중요하다.
앞으로의 개념들도 이런게 많은데, 식에 이런저런 변형을 가해서 tractable하게 만드는 것이 강화학습에서 중요한 개념 중 하나이다. 후에 policy gradient theorem도 이런 식으로 trick을 가해서 계산할 수 없는 것을 계산할 수 있게 만든다.

Bellman Optimality Equations
당연히 강화학습은 뭐가 optimal한지의 문제이기 때문에, optimality에 관심이 있다.
어떻게 시작할거냐면, 최고의 state-value는, 그 state에서 최고의 action을 취했을 때 나온다는 생각에서 시작할거다. 가장 행동을 잘 하면 그 상태에서 가장 최고값을 끌어낼 수 있으니까.
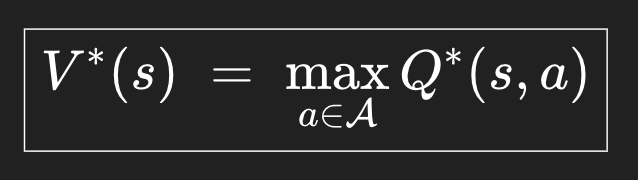
그리고 최고의 action-value는, 그 action을 취한 보상을 받고, 그 뒤의 reward들이 모두 최고의 value가 나오면 그게 그 action을 취했을 때 나올 수 있는 최고의 action-value라는 생각을 할 수도 있다.
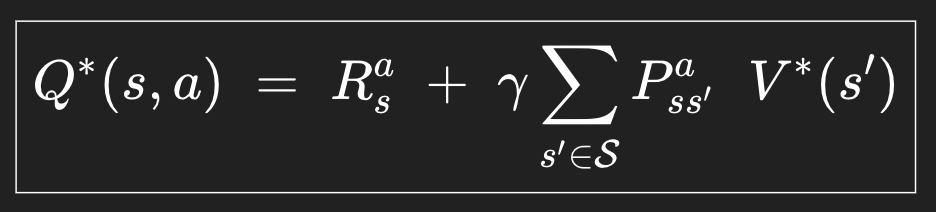
그런데 아까 Bellman Expectation equation에서 각각 뒤에 있는 Q랑 V를 대체할 수 있었다. 대체해보자.

이게 우리의 optimal한 값을, 각각 다음 step을 이용해서 나타낸 수식이다. 그래서 요걸 재귀적으로 풀어내면, optimal한 값을 구할 수 있다. 나이스...?
No Closed Form Solution
가 아니다.. 식에 보면 max가 있는데, 이 max 때문에 linearity가 깨져버려, closed solution을 찾지 못하는 상황이 발생한다.
대체 왜..?
그 대신, 우리가 rely 할 수 있는 딱 하나는, 우리가 discount되는 감마를 가지고 있다는 것이다.
만약에 linearity가 있었다면, 그냥 inverse matrix 이런걸로 한 방에 값을 구할 수 있었을 것이다. 하지만 그런건 없고, 가진건 0에서 1사이의 감마 뿐이다.
하지만 이 0에서 1 사이의 감마는, contraction mapping을 해주기 때문에 계속 iterate하면서 업데이트 하면 특정 fixed solution으로 가게 할 수 있다. ‘bootstrapping’ 을 통해서, 우리의 guess를 계속 하나하나 업데이트 해가면서, solution에 도달하는 것이다.
왜 contraction mapping이 특정 solution에 도달하나요?

어지럽게 보지말고, 밑에 T를 적용하여 매핑한 결과가, 최소한 감마만큼 보다는 더 작은 거리를 가진다는 걸 알 수 있다. 이렇게 되면 우리는 iteratively하게 T (Bellman optimality equation이다) 를 적용하면, 계속 거리가 짧아지고, 결국에는 fixed point로 converge 할 수 있는 것이다.

이 T (Bellman operator)를 contraction mapping이라고 하는 모양이다.
결국,

Single limit인 V optimal로 가는 모양이다. Supremum norm 이거는 optimization theory 시간에 봤던 것 같은데, 매핑하는 것도 그렇고 optimization theory의 냄새가 진하게 난다..
이걸 위해 다양한 방법들이 있는데,

이는 다음 게시물에서 알아보자. 다음은 매우 classic한, common approaches of RL에 대해 다뤄볼 것이다.
'Agent AI (RL)' 카테고리의 다른 글
| A (Long) Peek into Reinforcement Learning -Part5 (0) | 2025.05.30 |
|---|---|
| A (Long) Peek into Reinforcement Learning -Part4 (0) | 2025.05.27 |
| A (Long) Peek into Reinforcement Learning -Part 3 (0) | 2025.05.22 |
| A (Long) Peek into Reinforcement Learning -Part 1 (3) | 2025.05.20 |
| Deterministic vs Stochastic policy (0) | 2024.03.08 |


