이전에 강화학습에 대해서 공부하다가 굉장히 좋은 글을 찾았는데, 영어로 되어있는 터라, 직접 공부하여 얻은 직관들도 좀 같이 써넣을 겸, 한국어로도 자료를 남길 겸 정리를 좀 해보려고 합니다. 또한 본인도 약간 신나는 감이 없지 않아 있는데, 인공지능에 입문하게 된 계기가 당연히 2016년 구글 딥마인드 챌린지 매치, AlphaGO 이기 때문입니다.
그전부터 딥마인드는 DQN을 이용해 Atari를 하는 등 강화학습의 대가적 모습을 보여주었고 (David Silver와 같은 사람들 덕분이겠죠) , AlphaGo로 대박을 터뜨렸으며, 인간의 기보도 필요없으면서 좋은 성능을 보이는 AlphaZero를 내고, DOTA2에서 프로선수들을 이겼습니다. OpenAI의 ChatGPT도 그 학습에 RLHF, 인간 피드백을 이용한 강화학습을 사용하며, 또한 최근 화제가 된 DeepSeek 또한 강화학습을 이용했다는 점, 또한 LLM을 넘어서 로봇과 같은 하드웨어에도 인공지능을 적용하려면 대부분 강화학습을 사용한다는 점 등은 강화학습의 중요성을 충분히 나타낸다고 볼 수 있습니다. 이번에 Deepmind에서는 행렬 간의 곱셈을 하는 혁신적인 방법을 AlphaZero에서 발견한 방법론을 이용해 알아내기도 하였고, AlphaProof는 수학 올림피아드 수준의 문제를 효과적으로 풀어내기도 합니다. 그리고 대부분의 Decision-Making에는 강화학습이 쓰이는 걸 볼 수 있는데, 이는 나중에 인간 사회에서 쓰일 정책을 내주는 AI 모델 같은 곳에서도 활용될 수 있을 것입니다.
저만의 강화학습에 대한 긴 intro를 뒤로하고, 강화학습의 기본적인 개념들, 그리고 고전적인 방법론들에 대해서 저자의 내용과 함께 제 사족과 직관을 더해 같이 알아보도록 하겠습니다.
- with respect to the lilianweng.
What is Reinforcement Learning?

어떤 Agent가 unknown environment에 놓여져 있고, 그 environment와 상호작용하면서 어떤 reward를 얻을 수 있다고 해보자. 그럼 그 agent는 획득 가능한 보상이 가장 커지도록, cumulative reward를 가장 maximize하도록 전략을 짤 수 있을 것이다. 이 전략을, 여러 번의 experimental trial과 피드백으로 가장 optimal하게 짜는 것이 바로 RL이다.
RL: 에이전트가 환경(Environment)과 상호작용하면서 장기적인 누적 보상(즉, 미래에 받을 보상의 합 혹은 기대값)을 최대화하는 최적의 행동 정책(Policy)을 학습하는 과정
이것 때문에 이 글의 카테고리가 Agent AI인 것이다. 결국 에이전트가 환경에 이리저리 들이받아 보면서 최적의 전략을 짜보는 것이다.
Key Concepts
일단 agent가 알려진/알려지지 않은 environment에서 어떤 action을 취하기 때문에, 이걸 나타내기 위해서는 우선 state, action, reward가 필요하다.
- State ((s_t)): Agent가 t 시점에서 관찰한 environment.
- Action ((a_t)): state ((s_t)) 에서 agent가 취하는 행동.
- Reward ((r_{t+1})): Agent가 action ((a_t)), 를 하고, ((s_{t+1})) 로 갔을 때 얻는 보상.
결국 하나의 timestep에서 일어나는 것들은, (어떤 s에서, a 행동을 취하고, r의 보상을 얻는다) 가 된다. 이를 간단히 표현하면, (s, a, r) 이며, agent가 경험하는 것들이다. 이것을 episode, 또는 trajectory 라고 부르며, agent의 경험은 이것들의 연속이다.

우리는 최종적으로 보상이 가장 커지는 행동을 원한다. 그게 가장 좋은 행동일 것이기 때문이다. 그렇다면 최종적으로 우리가 얻게되는 reward는 "Return" 으로, 다음과 같이 표현할 수 있다.
Return

- ((t)) 에서부터 시작하는 총 누적 보상이다.
- ((\gamma\in[0,1])) 는 discount factor이다.
왜 discount factor 감마를 쓰는가? 사람들은 가끔씩 단기적인 보상을, 먼 미래에 주어지는 보상보다 우선시할 때가 있다. 그럴 때 감마 값을 작게 만들면 미래 보상을 좀 무시할 수 있고, 단기적인 보상만 고려하도록 모델을 만들 수 있다.
감마의 변화에 따라 최종 보상 값이 어떻게 바뀌는지에 대한 직관을 위해, 아래와 같은 예시를 보면 된다.
시간이 t = 1, 2, 3, 4 이고 각각 나오는 보상이 [0, 3, 5, 10] 이라고 해보자.
t = 1에서 보상이 0이므로 단기적인 보상을 우선적으로 고려하게 되면 (감마 값이 작으면) 최종 보상이 낮을 것이다.
다음은 감마 값이 0에서 0.99로 점차 변하면서 최종 누적 보상이 얼마가 되는지를 나타내는 그래프이다.
감마를 0으로 해서 초단기적인 보상만 집중하니 최종 보상이 0이고, 0.99로 하니 미래 보상까지 다 집중해서 모든 보상들의 합에 가까워지는 것을 볼 수 있다 (보상총합이 18인데 17.5가 나오는 모습) .

그리고 return의 식을 보면 sum이 무한까지 가는 걸 볼 수 있다. 이런 상황에서 감마 = 1 일 경우, MDP 문제 중 infinte horizon sum reward criteria 에 속하는데, 간단하게 말하면 sum이 converge 되지 않는다는 뜻이다. optimization에 좋지 않을 것이다. 그래서 감마를 1보다 작게 만들어서, 우리의 문제를 infinite horizon discounted reward critieria로 만들어주는 것이다.
Model: State-Transition Probability & Reward function
모델이라 함은 environment에 대한 서술이다. 이 모델은 크게 두 구성으로 되어있는데, Transition Probability와 Reward function이 그것들이다.
State-Transition Probability
state-transition probability는 어떤 state s에 있는데, 이때 action a를 했을 때, 어떤 다른 state s'로 넘어갈 확률이다.
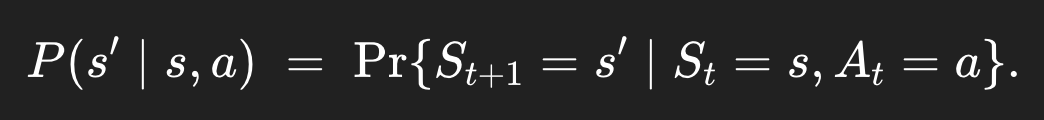
위와 같이 두 가지 방식으로 표기가 가능하다. 물론 한 가지 방식이 더 있는데,

이렇게이다. 왜 그런가 보면, P(s', r | s, a)는 어떤 상태 s와 action a가 주어졌을 때 어떤 새로운 상태 s′와 특정 reward r이 나올 확률을 알려준다. 근데 지금은 우리는 특정 reward까지는 필요없다. 그냥 새로운 상태 s'에 도착할 확률만 알면 된다. 그러니까 모든 특정 reward r의 경우의 수를 고려해주는, marginalization을 reward에 대해 해버리면 된다.
예시)
예를 들어, 나올 수 있는 모든 reward가 -1, 0, 1 밖에 없다고 해보자. 그러면

reward가 -1이면서 다음 상태 s'로 넘어갈 확률 + reward가 0이면서 다음 상태 s'로 넘어갈 확률 + reward가 1이면서 다음 상태 s'로 넘어갈 확률 = 그냥 다음 상태 s'로 넘어갈 확률
이게 marginalization이다.
Reward function
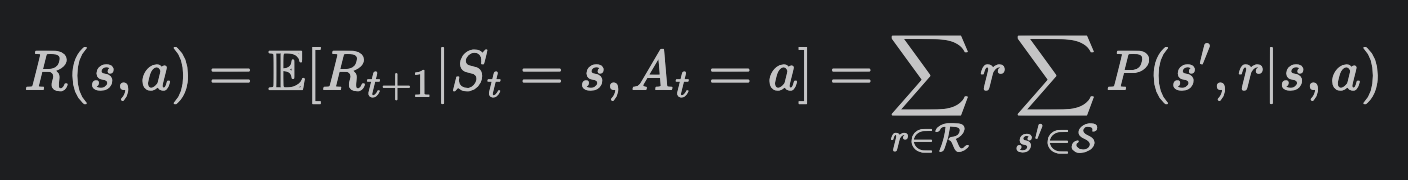
우리의 reward는, 어떤 state s에서 action a를 했을 때, 나올 수 있는 총 보상이다.
이건 가장 오른쪽의 식에서 볼 수 있듯이,
어떤 state s에서 action a를 했을 때, 다음 state로 갔을 때에 나오는 총 보상을 구해야 하므로,
일단 state s에서 action a를 했을 때 다음 state와 특정 r을 얻을 확률에다가, 당장 다음 timestep의 모든 state에 대해 다 고려할 것이니까 sum, 그리고 거기서 나오는 특정 r이 아닌 모든 r에 대해서 고려할 거니까 sum 이렇게 해주는 것이다.
Policy
Policy는 agent의 행동양식에 대한 함수이며, 파이로 나타낸다. 어떤 state s를 action a로 매핑해주는 함수이다.
본인은 이 개념에 대해서 처음 들여다볼 때 매우 헷갈렸는데, "확률" 이다. 물론 deterministic한 case에 대해서는 Policy는 action a를 뱉어내고, stochastic한 case에서는 여러 action이 각각 나올만한 확률분포를 뱉어내지만, 대부분의 경우에서 우리는 stochastic한 경우를 많이 볼 것이므로, 여러 action들이 나올 확률이라고 보면 된다. 우리는 agent가 최적의 행동양식을 가지길 원함으로, optimal한 policy를 원한다.
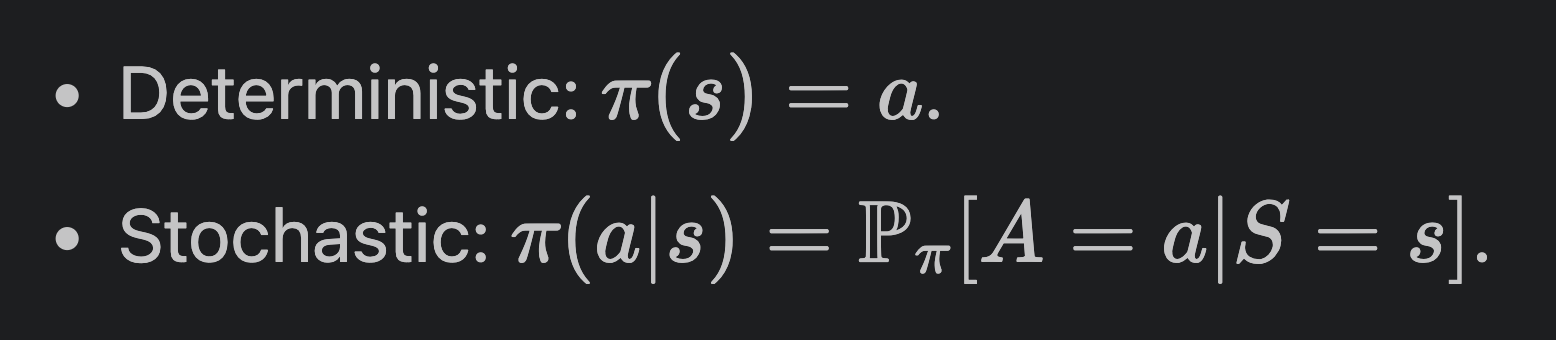
매우 직관적인 이해는 다음과 같다.
어떤 state s를 받아서 (이 state 안에서) action들의 확률분포를 뱉는 것이 policy라고 보면 된다.
어떤 state s에서 가능한 action의 종류가 위로, 아래로, 왼쪽으로, 오른쪽으로 만 있다고 해보자.
Policy의 한 예시로는,
위로 갈 확률 10%, 아래로 갈 확률 30%, 왼쪽으로 갈 확률 40%, 오른쪽으로 갈 확률 20% 인 정책 을 들 수 있다.
확률분포를 뱉는다는 것은 이런 의미이다. agent가 어떻게 행동해야 하는지에 대한 정책이다. 우리는 optimal한 policy를 원한다.

Value function
value function은 말 그대로 가치를 측정하는 함수이다. 어떤 state가 얼마나 좋은지, 또는 어떤 action이 얼마나 좋은지를, 거기서 시작해서 발생하는 모든 미래 reward를 다 합해서 value를 측정한다.
우리의 return은 다음과 같았다.

어떤 state가 얼마나 좋은지, state-value 는 다음과 같다:

어떤 action이 얼마나 좋은지, action-value (Q- value) 는 다음과 같다:

식을 잘 보면 모두 Expectation이 쓰였는데, state-value에서는 상태 = s 로 주어졌을 때의 expected Gt 값을, Q-value에서는 상태 = s와 특정한 action = a 로 주어졌을 때의 expected Gt 값을 뜻하는 식들이다. 식은 복잡하지만, 직관적이다.
여기에 더하여, Q-value를 이용해 state-value를 알아낼 수 있다. 위의 policy를 다시 한 번 생각해보자. policy는 action들에 대한 확률분포였다. 그리고 Q-value는 action의 가치이다. 그러면 한 state에서 가능한 모든 action들이 각각 일어날 확률과, 이에 대한 각각의 value도 있으니, 그걸 조합하면 한 state에서의 value를 얻을 수 있지 않을까?
이는 다음과 같다:

일단 하나의 action이 일어날 확률에 그 가치를 곱하면 그 action이 주는 기댓값을 구할 수 있으며, 이걸 모든 action에 대해 sum 해주니까 state-value가 나올 수 있는 것이다.
강화학습은 경험 상, 수식이 복잡하기 때문에 그냥 머리에 외우려고 하면 쓸데없고, 까먹고, 괜히 '아 나 식 모르는데.. 너무 복잡한데..' 이렇게 되어버린다. 위의 서술처럼 직관적인 이해가 중요하다고 생각한다.
Advantage
위의 Q-value에서 State-value를 빼면 Advantage라고 하는 값이 나온다.

이건 왜 있냐면,
V(s)는 그 상태가 기본적으로 얼마나 좋냐,
Q(s, a)는 그 상태에서 어떤 행동을 했을 때 그 행동이 얼마나 가치를 변화시키느냐,
이기 때문에, policy에 따른 state의 기본값에 비해서 어떤 action이 얼마나 좋냐/나쁘냐 를 상대적으로 볼 수 있다. 직관적으로 말하면, 기본일 때에 비해서 딱 요 action이 가지는 장점만 쏙 뽑아낸 것이다.
이거 나중에 매우 자주 보게 될 것이다. Policy Gradient로 들어가기 시작하면 gradient의 variance를 줄이기 위해서 사용하기 때문이다. 간단하게만 얘기하면 이 state가 얼마나 좋은지, 기본적인 baseline 값에 대해 상대적인 것만 봄으로써 gradient signal을 "center" 할 수 있고, variance를 줄여준다. 약간 normalize 같은 느낌이라고 보면 될 것이다.
Optimal Value & Policy
강화학습은 결국 optimal한 걸 원하기 때문에, 대체 뭐가 optimal한 거냐? 에 대한 기준을 세워야 한다. 이걸 만족하면 그게 최적의 value이고 최적의 모델 행동양식이기 때문이다.
Optimal Value function

당연히 둘 다 value가 max되는게 optimal한 value function일 것이다.
Optimal Value and Policy

당연히 optimal한 policy를 따르면, 최적의 행동양식을 따르면, 가장 높은(optimal) value가 나올 것이다.
위는 그냥 max였지만 여기서는 argmax인 점에 유의하자. Value를 가장 높게 만들어주는 특정한 파이 값이라고 해석하면 된다.
https://lilianweng.github.io/posts/2018-02-19-rl-overview/#key-concepts
A (Long) Peek into Reinforcement Learning
[Updated on 2020-09-03: Updated the algorithm of SARSA and Q-learning so that the difference is more pronounced. [Updated on 2021-09-19: Thanks to 爱吃猫的鱼, we have this post in Chinese].
lilianweng.github.io
'Agent AI (RL)' 카테고리의 다른 글
| A (Long) Peek into Reinforcement Learning -Part5 (0) | 2025.05.30 |
|---|---|
| A (Long) Peek into Reinforcement Learning -Part4 (0) | 2025.05.27 |
| A (Long) Peek into Reinforcement Learning -Part 3 (0) | 2025.05.22 |
| A (Long) Peek into Reinforcement Learning -Part 2 (0) | 2025.05.20 |
| Deterministic vs Stochastic policy (0) | 2024.03.08 |
