[ECCV 2014] Visualizing and Understanding Convolutional Networks (DeConvolution)

 

오늘은 deconvolution에 대해 다뤄보려고 한다. 편하게 그냥 deconv라고 하겠다.

 

이름에서부터 알 수 있듯이 CNN 속의 과정을 탐구하는 방법론이며, 이미지를 받아서 줄이고 줄이고 줄여가는 CNN과 반대로 우리가 관심이 있는 어떤 단계의 줄여진 친구를 다시 늘리고 늘리고 늘려가면서 최종적으로 히트맵을 출력, 특정 단계에서의 CNN이 어떤 부분에 집중하고 있는지를 알 수 있는 방법론이다. 

 

논문 원문은 다음과 같다.

https://arxiv.org/abs/1311.2901

Visualizing and Understanding Convolutional Networks

 

---

 

논문의 의의

 

이번에는 구체적인 과정보다 논문의 의의를 먼저 다루고 시작하겠다. DeConv가 가져온 의의는 몇 가지가 있는데, 다음과 같다.

• Switch-Based Unpooling
• Non-Parametric Feature Projections
• Layer-Wise insights

일단 Switch-Based Unpooling은, "Switch"라는 걸 이용해서 Unpooling, 즉 다시 늘렸다는 것이다. 이 스위치는 pooling할 때 (이미지 줄일 때) 가장 큰 값의 위치를 저장해주는 "무언가" 이다.

 

이 스위치를 구현하는 방법에는 여러 관점에 따라 여러 가지 방법이 있는 듯 한데, 일단은 pooling할 때의 가장 큰 값을 저장해준다고 생각하면 된다.

 

여러가지 관점에 따른 스위치 구현하는 방법 

2x2 max-pooling layer라고 예시를 들어보자. (2x2 네모 속에서 가장 큰 값 하나만 남기고 나머지는 없애서 줄인다는 뜻이다)

 

1. Binary Mask의 point of view에서 switch 구현하는 방법

 

이 경우 직접적으로 벡터를 가리는 "Mask"를 apply 해주는 것이다.

 

 

2. Coordinate Map의 point of view에서 switch 구현하는 방법

 

이 경우 그냥 가장 큰 값의 좌표를 저장해두는 것이다.

스위치를 통해 최대값이 어디에 있었는지 알고, spatial information을 보존하므로 좀 더 좋은 reconstruction이 가능하다는 것에 의의가 있다.

 

Non-parametric featur projections에 대해서는, 다른 gradient-search method들과 다르게 따로 pixel space에서 optimization 해줘야할 것이 없다. 따로 파라미터도 존재하지 않고, 그냥 이미 학습되었던 operation들을 reverse하기만 하면 된다. 그렇기 때문에 파라미터에서 자유롭다는 뜻이다.

 

그리고 마지막 부분이 좀 중요하다고 생각하는데, CNN의 각 layer가 대충 무슨 일을 하는지에 대한 감이 잡히기 시작했다. 논문의 사진을 보자.

 

 Layer 1에서 보이는 패턴들은, 대각선 직선 모양이거나 뭔가 직선으로 반반 나뉜다거나와 같은 패턴을 보인다. 여기서 중요한건? "직선"의 모양이라는 것이다.  Layer 2를 보면 뭔가 곡선도 들어가고 원도 생긴다. Layer 3을 보면 벌집같은 모양도 보이고, 좀 더 기하학적인 모양들도 보인다. 몇 개는 형체 같은 것도 보이는 것 같기도 하다. Layer 4와 5를 보면 점점 더 복잡해지고, 뭔가 모양이 점점 더 구체적으로 바뀐다. 이게 DeConvNet의 contribution인데, CNN의 초기의 layer들은 상대적으로 단순한 패턴을, 그리고 깊어질 수록 좀 더 복잡한, hierarchical한 구조를 지니며 이미지를 파악한다는 걸 알아낸 것이다.

 

---

 

Detailed DeConv process

 

대충 뭐하는 건지는 알았으니, 이제 어떻게 하는지에 대한 순차적인 방법으로 들어가보자. 다행히도 저자들이 친절하게 과정에 대한 figure를 수록해놓았다.

 

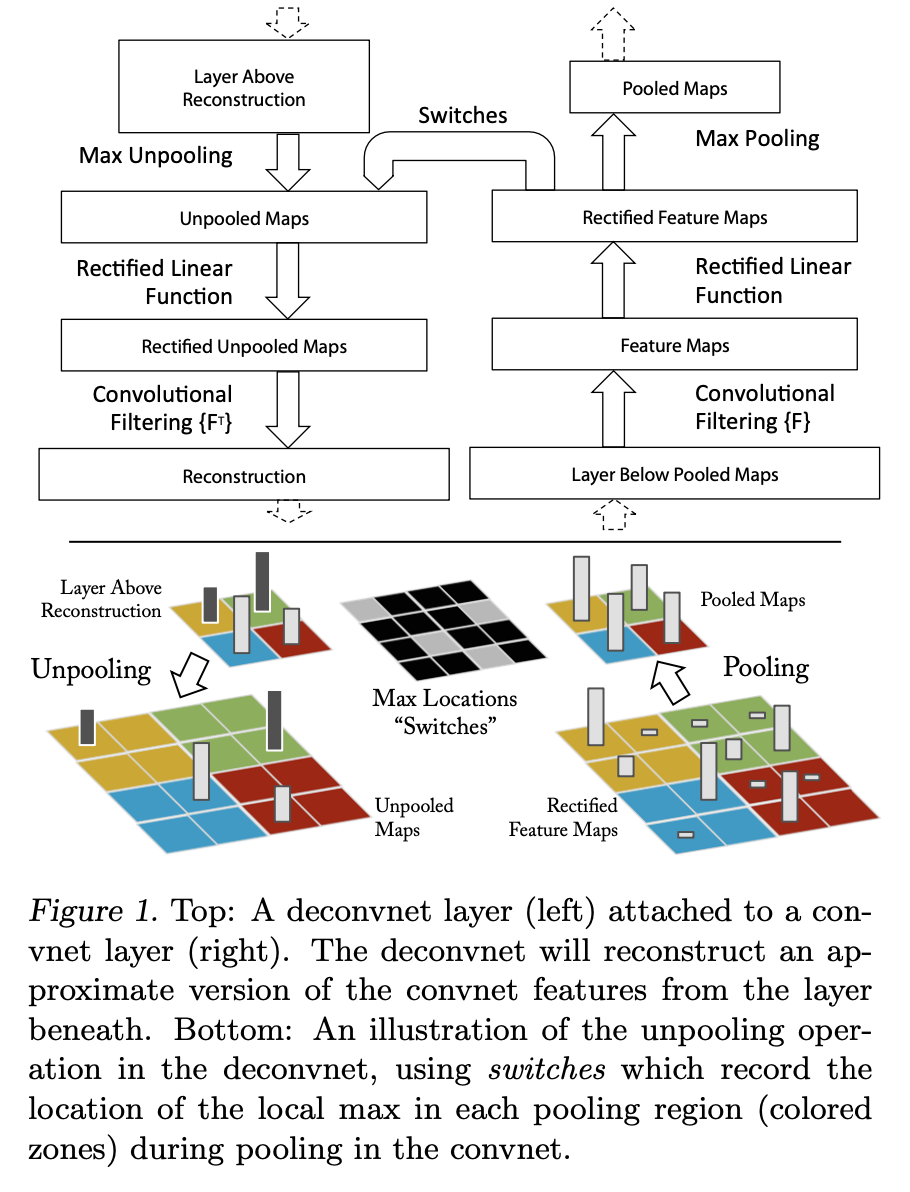
하지만 이 그림만 보고 모든게 다 이해되면 이 블로그를 읽을 이유도 없고 필요도 없다. 과정 하나하나씩 뜯어보자. 

 

1. Forward Pass, Switch Recording

2. Selecting and Masking a Single Activation

3. Unpooling (Using Switches)

4. ReLU apply (Rectification)

5. Deconvolution (Filter-Transpose)

6. Iterate Downwards

 

DeConvNet의 과정은 위와 같다. 

 

1. Forward Pass, Switch Recording

 

일단 모델을 돌려야 deconv를 하던지 말던지 한다. 그래서 모델에 이미지를 넣고 원래 하던대로 각 layer 별로 계산을 해준다. 이 과정에서 "Switch"를 기록할 거다. Max-pooling이 feature map을 downsample할 때마다, (2x2 kernel을 통해 8x8 -> 4x4) 나온 값 (4x4에 기록된 값, 얘네들이 각자 2x2 영역에서 가장 큰 값, 즉 argmax였을 테니)의 위치를 기록한다. 이렇게 switch를 만든다. 

 

2. Selecting and Masking a Single Activation

 

그 다음에 우리가 알고 싶은 특정 레이어의 하나의 뉴런 값을 고른다. 그리고 feature map 전체에다가 통째로 mask를 씌워버린다. 그러면 그 layer에서 다른 activation들은 다 지워지고 (zero-out), 모델이 오직 내가 원하는 값만 propagate 할 수 있게 된다. 이게 바로 DeConv가 LIME이나 SHAP와 같은 XAI 방법론의 분류 중 Perturbation based method 라고 불리는 이유이다. 이 masking을 통해 이미지에 변화를 주어 우리가 원하는 걸 알 수 있게 만드는 것이다. 

 

3. Unpooling (Using Switches)

 

Unpooling은 어떻게 하는거냐면, 우리가 기록해뒀던 argmax가 있었던 자리에 값을 넣어주고, 그게 예를 들면 2x2 영역에서의 argmax값이었다면, 그냥 그 주변의 2x2 영역을 0 값으로 채워주는 것이다. 

 

4x4인 feature map을 2x2 max-pooling 해보자.

 

이렇게 될 것이다. 각 2x2에서 제일 큰 숫자만 골라왔다. 그리고 그 위치를 "스위치" 로 기록한다.

argmax 숫자가 있던 곳에 1

 

하지만 여기서 2번 과정을 다시 보면, single activation만 보통 선택한다고 했다. 예를 들어 위에 있는 숫자 6 부분이 알고 싶다고 가정해보자. 그러면 6 빼고 다 0으로 만들어줄테니까, 다음과 같다.

 

그리고 6만 남았으니까, 우리의 switch도 6의 위치만 간직하면 된다 (1,1).

 

 

4. ReLU apply (Rectification)

 

위의 결과물에 ReLU 적용해준다. 음수를 0으로 만들어주면 된다. 지금은 음수값이 없으니 그대로일 것이다. 

 

5. DeConvolution (Filter-Transpose)

 

이제 deconv 연산을 수행해주면 되는데, 이거는 transpose된 filter matrix를 곱해주면 된다. 왜 전치된 필터를 곱해주냐면, 우리가 그 convolution step을 "inverse" 해주고 싶기 때문이다. 결국 행렬 연산이기 때문에 전치된 친구를 다시 적용해주면 돌려놓을 수 있다고 원상태로 돌려놓을 수 있다고 보면 된다. 

 

다시 위의 예를 사용해보자. 우리가 4x4를 max-pooling 해서 2x2로 만들었다. 그리고 DeConvNet에서 4번 과정까지 한 결과 Unpooling된 4x4를 다시 만들어줬다. 그러면 이제 이렇게 나온 4x4를 다시 늘려야한다. 원래 이미지 크기가 될 때까지. 이거를 하려면 원래 4x4에 적용된 filter(학습된 filter)를 가져와서 그거의 전치행렬을 곱해주면 된다. 

 

 

이렇게 생긴 3x3 filter를 이용하여, 6x6의 feature map을 4x4로 줄여줬었다고 해보자. 

 

그러면 적용했던 filter의 transpose는 다음과 같고,

 

위의 전치된 filter랑 다시 convolution 연산을 수행해주면 된다.

 

과정은 조금 끔찍하다.

 

이렇게 해서 다시 6x6으로 복구했다.

 

6. Iterate Downwards

 

당연히 여러 개의 필터가 있고 이미지가 줄어드는 과정도 여러 번 있기 때문에, 원본 이미지의 크기가 나올 때까지 위의 과정을 반복해주면 된다. 

 

---

 

Deconvolution 단점

 

단점들도 당연히 있다.

 

1. Approximate, Not Exact Inversion
   – Max‑pooling and ReLU are many‑to‑one operations (they throw away information), so any “unpool → ReLU → filter‑transpose” pipeline can only approximate the true inverse. Reconstructions are suggestive, not exact reconstructions of what the network “saw.”
2. Drops Negative Contributions
   – Because deconvnets reapply ReLU at every backwards step, they only visualize positive activations. Any inhibitory (negative) evidence contributing to a neuron’s decision is lost.
3. Single‑Unit Focus
   – Standard deconv visualizations zero out all but one activation. They therefore ignore interactions among multiple neurons or feature maps, missing the combined patterns that actually drive a decision.
4. Sensitive to Architecture & Hyperparameters
   – The fidelity of deconv projections depends on pooling window size, stride, and filter dimensions. Small changes (e.g. overlapping vs. non‑overlapping pooling) can drastically alter the switches and thus the visualizations.
5. Computational & Memory Overhead
   – Attaching a full deconvnet to every layer—and replaying unpooling, rectification, and transposed convolutions—adds significant runtime and storage, complicating large‑scale or real‑time applications.
6. Ignores Normalization & Shortcut Paths
   – Layers like batch/contrast normalization or residual connections have no straightforward inverse in the deconvnet, so many modern architectures cannot be faithfully “rewound” end‑to‑end.
7. Potential for Misinterpretation
   – Because deconv visualizations spotlight the strongest activating patterns, they may over‑emphasize edges or textures and under‑represent broader contextual cues the network also uses.
8. Limited to Convolutional Layers
   – Deconvnets focus on feature maps and do not naturally extend to fully‑connected layers, attention modules, or non‑convolutional architectures (e.g. transformers), limiting their applicability to older CNN designs.