지금까지 우리는 "Value-based" RL을 보았다. Q-function을 approximation해서 가치를 추정한 다음에, 이를 바탕으로 policy를 구하는 과정이었다. 그래서 항상 흐름도 V(s)를 구하거나, Q(s,a)를 구한 뒤, epsilon-greedy 이런 식으로 policy에 대해서 다루었다.
근데 여기서 의문이 생기는 것은, 그냥 policy를 또 parameterized function으로 직접 구해버리면 안되나?
이런 내용일 것이다. 이러한 의문점에서 파생된 것이 바로 "Policy-based" RL이며, 지금부터 볼 policy gradient를 기반으로 한 알고리즘들이 바로 그것들이다. (당연히 gradient가 들어간다, parameterized function은 또 딱 봐도 neural network 쓸 것이고, 그러면 gradient가 필요하다)
Our Goal
일단 우리가 뭘하고 싶은지, 뭘 최적화할 지 목표를 세워야된다.
다음에 따라, environment와 상호작용하면서, experience들을 모아서 trajectory를 만들 수 있다.
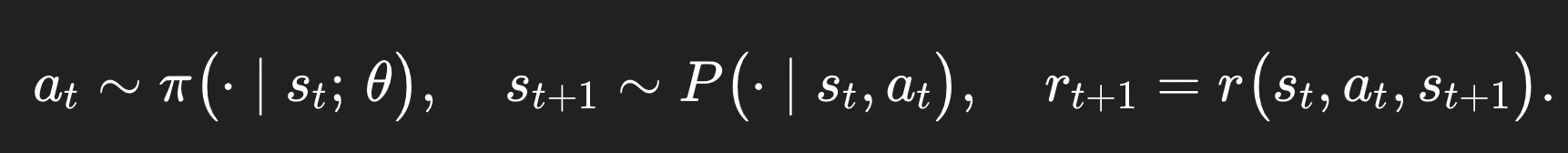
그러면 어떤 policy π 를 따르는 complete trajectory τ (타우)가 다음과 같을 것이다.

그러면 저 trajectory가 얼마나 가치있는지에 대한 τ trajectory의 complete return은 다음과 같을 것이다. (t=0 부터 시작해서 나오는 모든 return 합친 것이다) (대문자 T는 terminal state이다)
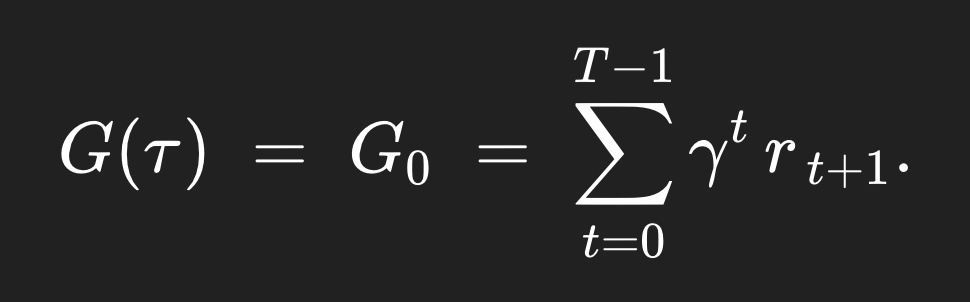
위에 저 τ trajectory의 가치가 얼마나 되는지를 구했으면, 이제 그 τ trajectory가 어떤 확률로 발생할지도 한 번 알아보자.
p_θ(τ) 라고 표기할 것이다.

간단하다, 매 스텝마다 어떤 확률로 action을 고르고, 그 action으로 또 state가 넘어갈 확률도 있으니까 그 두 개를 곱해줬는데, 그게 여러 스텝이 있으므로 앞에 싹 다 곱해주면서 joint probability의 형태를 띈다. 그리고 initial probabilty까지 곱해주면, 어떤 특정 trajectory τ가 나올 확률을 위의 식처럼 알 수가 있다.
이제 우리는 위에 볼드체 처리해놓은 trajectory τ의 가치와, 그 trajectory τ가 나올 확률도 안다. 그러면 이를 통해,
어떤 policy π를 따라 나온 trajectory τ의 기댓값을 알 수가 있다.

그러면 당연히 우리의 목표는, 저 기댓값을 최대화 해주는 parameter theta를 찾는 것이 될 것이다.

그리고 이걸 위해서는 당연히, 이따가 왜 이 이야기가 나오는지 다루겠지만, "실제 계산 가능" 한, "tractable" 한

gradient가 필요하다.
이래서 "Policy Gradient" 가 나오는 것이고, 처음 보면 계산이 불가능해보이는 식이 나온다. 하지만 이걸 잡기술로 잘 우회해서 실제로 계산 가능하게 만들어주는 게 바로 "Policy Gradient Theorem" 이다. 맨날 말만 듣던 그 녀석들이 바로 이런 의미인 것이다.
Policy Gradient Theorem
매우매우 중요한 부분이다. 같이 하나하나 보도록 하자. 여기서의 핵심은 바로 저 위에 ∇θJ(θ)가 계산이 안되므로, Monte Carlo 방식을 이용해서 estimation할 수 있는 방식으로 수식을 전개하는 것이다.
*우리의 주요 목표는 Expectation을 밖으로 빼내고, gradient를 안으로 넣는 것이다.
*이렇게 되면 몇 개의 샘플링으로 gradient를 계산해서 expectation에 근접하도록 estimation을 할 수 있게 된다!
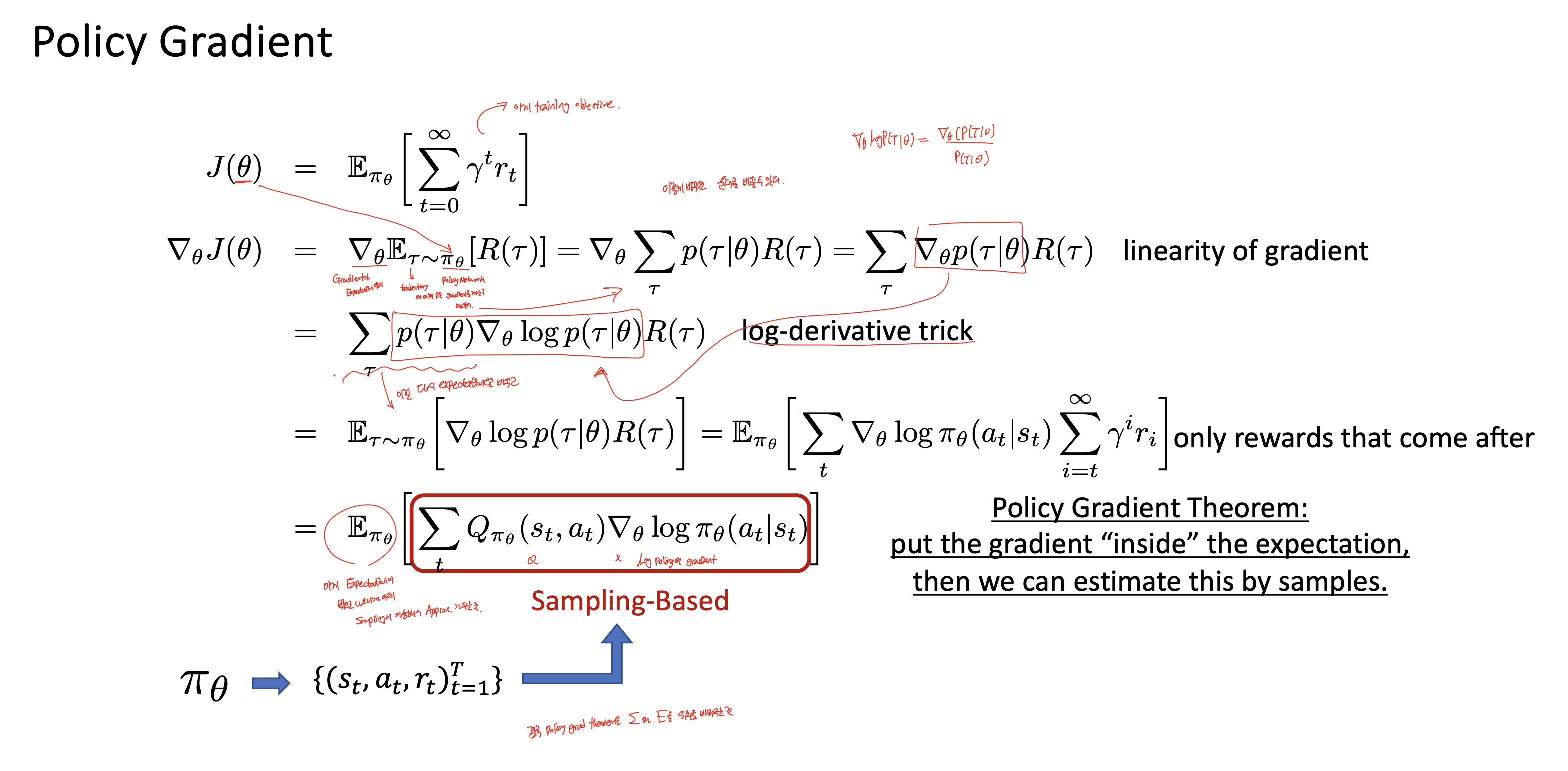
하나하나 살펴보도록 하자.
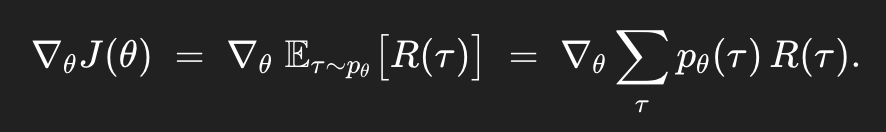
이렇게 sum으로 바꿔줄 수 있는 것은 τ가 discrete trajectory이기 때문이다.
그다음 linearity of gradient의 성질인데, 이건
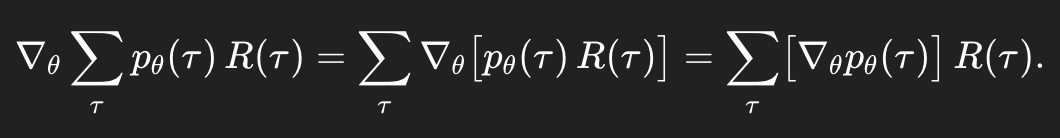
gradient를 sum 안으로 집어넣을 수 있다는 뜻이다. 왜? differentiation이 linear하기 때문이다.
가장 중요한 부분인데, log-derivative trick을 쓴다.

왜 이렇게 되냐면,

이 성질을 이용할 건데, 이건 log를 미분할 때의 성질에서 나온다.

이렇게 log-derivative trick을 이용하면 처음의 식이 다음과 같이 바뀐다.

근데 앞에 sum과 뭔가 확률이 곱해져있으니까, 이건 그냥 expectation이다. 그러면 이렇게 된다.

이게 왜 좋냐면, 이제 gradient가 expectation 안으로 들어가있다. 원래는 전체를 다 계산해서 expectation 한 것의 gradient를 구해야함으로, 난이도가 매우 어렵다(사실상 불가능). 근데 이젠 finite한 trajectory를 샘플링해서 gradient를 구하는 식으로 이걸 대체할 수 있는 것이다! 저 ∇θJ(θ)를 MC 방법으로 estimate할 수 있게 된다. tractable 하게!

근데 이 수식은


아래의 수식과 정확히 동일한 수식이다.
왜..?
그런데, 위의 수식은 또 다음과 같이 쓸 수 있다.
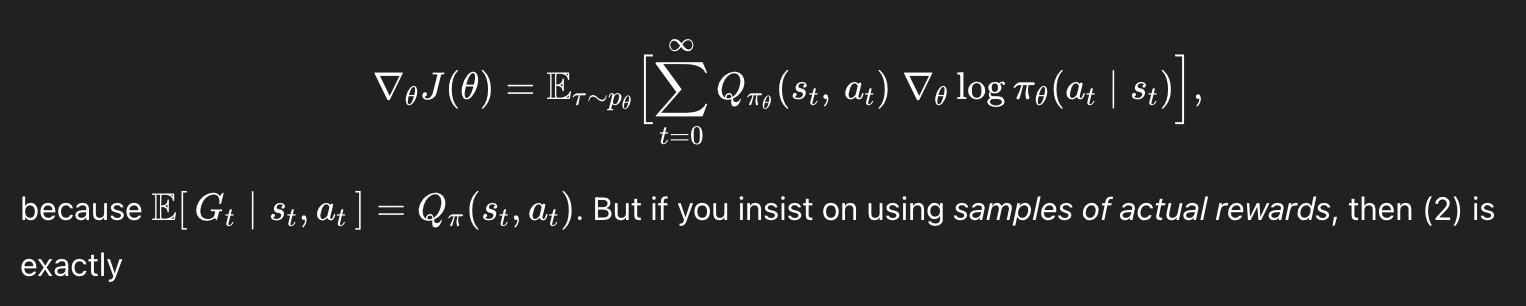
왜..?

그러니까 최종적으로 우리는 다음과 같은 식을 가진다.
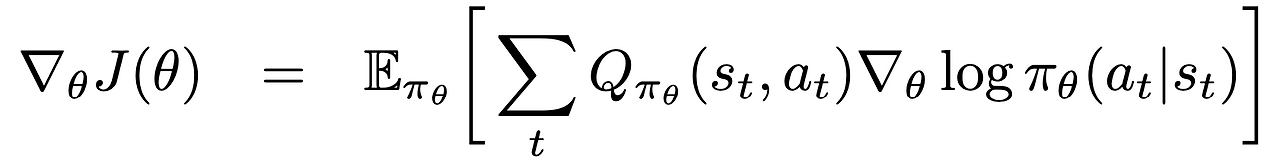
이제 우리는 드디어 sampling을 통해 계산할 수 있게 된 것이다!!
실제로 계산할 때는,

이렇게 empirical하게 계산하게 된다.
REINFORCE
위에서 우리가 Gt를 Q로 바꿔서 sampling을 통해 계산했다. 이게 바로 MC 방식의 REINFORCE 알고리즘이다.
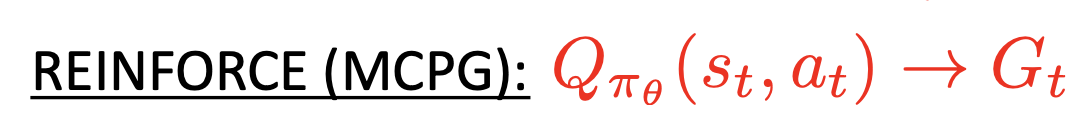


잘 보면 for each episode라고 적혀있으며, parameter theta의 업데이트가 에피소드가 끝날 때마다 이루어지는 것을 볼 수 있다. 이는 우리가 이전에 봤던 MC 방식과 같다. 참고로 헷갈릴까봐 덧붙이자면, 첫 번째 pseudocode의 optimize가 theta update와 같은 부분이다.
Conclusion 및 insight
앞으로 policy gradient를 이용한 알고리즘들, Q Actor-Critic, A2C, TD A2C, GAE, A3C 들은 전부 이 앞에 Q부분을 조작해서 조금씩 다르게 만든 것들이다. 그래서 앞으로 모든 것은 우리가 도출해낸 마지막 식에서부터 전개되므로, 잘 기억해놓는 것이 좋을 것이다.

(매우 중요!!)
'Agent AI (RL)' 카테고리의 다른 글
| A (Long) Peek into Reinforcement Learning -Part8 (0) | 2025.06.08 |
|---|---|
| A (Long) Peek into Reinforcement Learning -Part6 (0) | 2025.06.01 |
| A (Long) Peek into Reinforcement Learning -Part5 (0) | 2025.05.30 |
| A (Long) Peek into Reinforcement Learning -Part4 (0) | 2025.05.27 |
| A (Long) Peek into Reinforcement Learning -Part 3 (0) | 2025.05.22 |



