[CVPR 2020] Dynamic Convolution: Attention over Convolution Kernels

 

오늘은 Light-weight CNN에서 발생하는 performance degradation을 보완하기 위해 등장한 Dynamic Convolution 기법에 대해 알아보고자 한다. 

 

원문링크: https://arxiv.org/abs/1912.03458

Dynamic Convolution: Attention over Convolution Kernels

 

---

 

1. Background

 

MobileNetV3-Small 과 같은 Lightweight CNN들은 모델 자체가 크지 않고 가벼운 대신 당연히 성능이 떨어지는 문제가 있다. FLOPs budget을 맞추기 위해 모델의 depth나 width를 줄이면 모델의 representation power가 떨어지는 문제점이 있는데, 이에 Chen et.al은 모델의 depth와 width를 확장하지 않고, 소량의 computational cost의 증가를 통해 성능을 향상시켜주는 기법인 Dynamic Convolution을 제안한다.  

 

2. Method

 

Dynamic Convolution은 K개의 pararell 한 kernel을 사용한다. 이들은 모두 same spatial size와 same channel dimension을 가진다. 그림으로 먼저 보면 이해가 더 쉽다. 

 

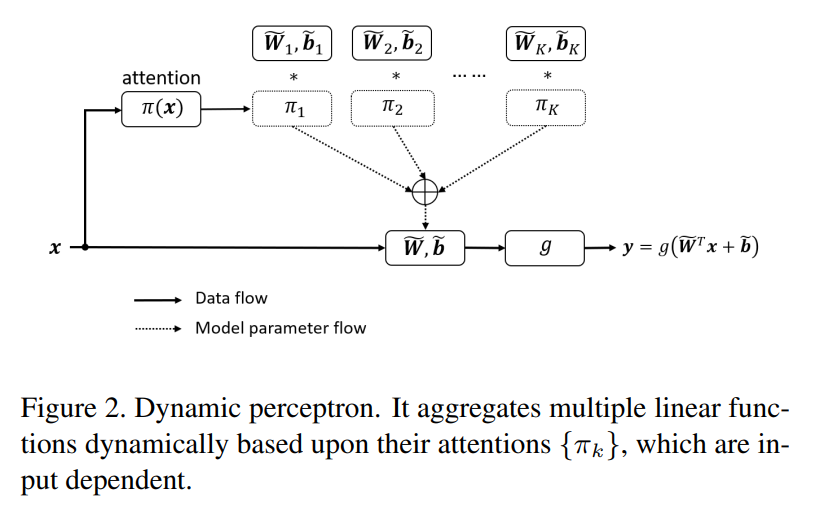
이건 저자들이 preliminary로 제시하는 dynamic perceptron의 구조이다. 이와 똑같은 원리로 dynamic convolution이 적용되는데, 먼저 perceptron 구조로 보는게 좀 더 편할 것이다. 위의 그림을 보면 여러 개의 W가 합쳐지면서 최종 W가 되고, 각각의 W에는 attention 가중치가 붙어있는 것을 볼 수 있다. 

 

그래서 K개의 

 

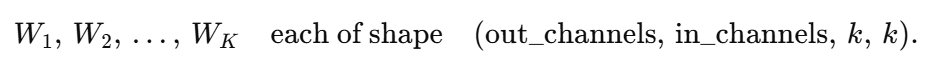
가 존재하며, 이들을 모두 합치는데, 앞에 가중치가 붙은 형태인

이렇게 최종적으로 나오게 된다. 

 

결국 한 layer 당 하나의 convolution kernel을 사용하는 대신에 K개의 병렬적인 kernel을 사용하겠다는 것이다. 

 

하지만 실제로 구현될 때는 convolution 연산을 K번 하는 것이 아니라, 합쳐놓고 최종적인 W를 single convolution으로 진행한다. 이는 후에 Dynamic Convolution을 볼 때 다시 이야기하도록 하겠다.

 

2.1 Dynamic Convolution

 

Dynamic perceptron을 보았으니 이젠 Dynamic Convolution을 보면 되는데, 같은 원리로 진행된다. 그림을 먼저 보자.

 

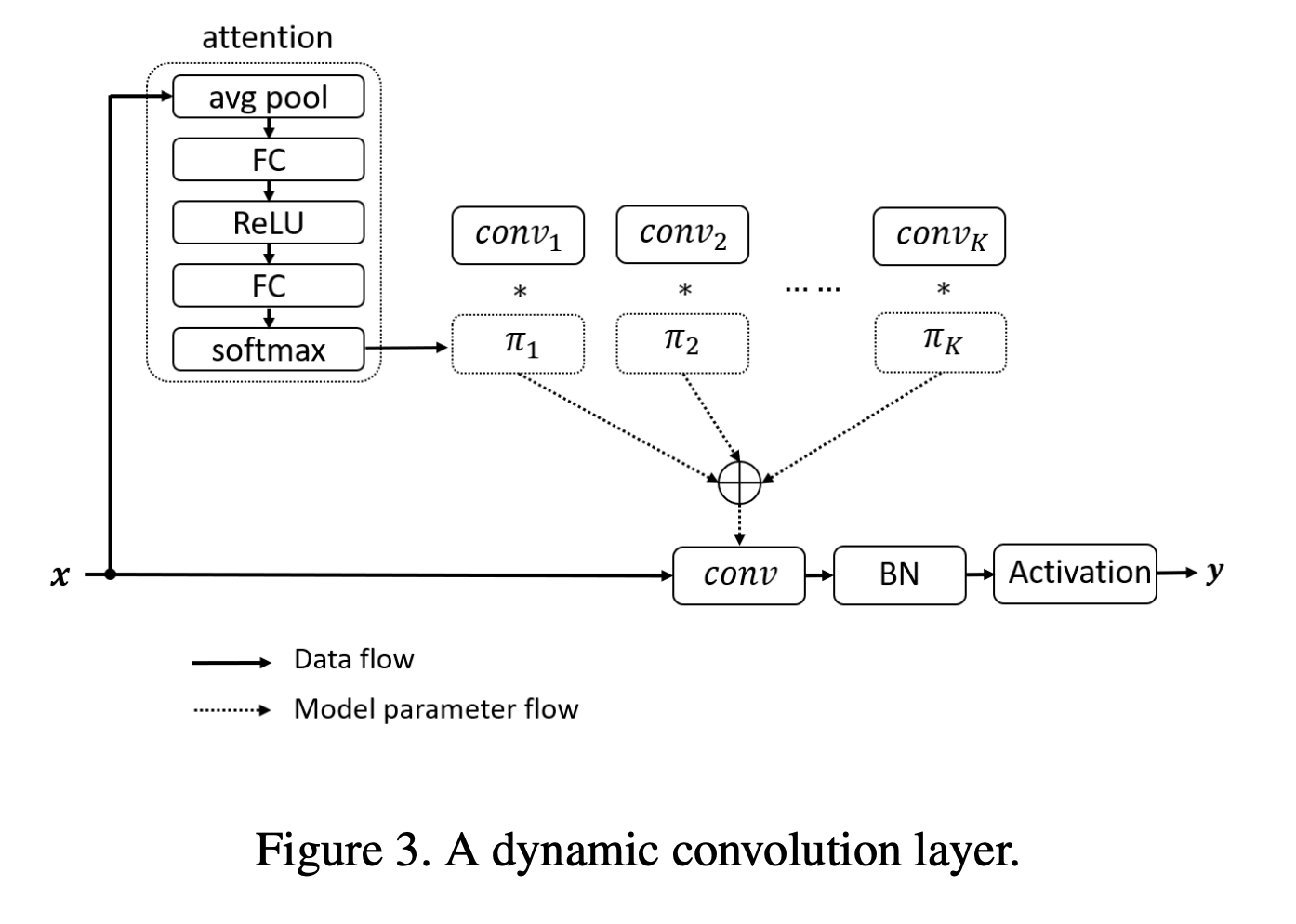
K개의 input/output dimension과 size가 동일한 Convolution Kernel을 가지고 있으며, 이 커널들은 attention weight π 를 이용해 합쳐진다. 아까 말했던 합쳐놓고 최종 single convolution으로 진행한다는 것이 바로 이것이다. π를 가중치로 해서 각 커널들을 전부 aggregate한 이후에 고전적인 CNN 형태로 batchnorm과 activation function (ReLU)를 통해 하나의 dynamic convolution layer를 만든다.

 

전체적인 과정을 한 번 쭉 보면, squeeze(avg pool) and excitation 과정을 거치고, kernel aggregation을 하고, 그 다음 single convolution을 하는 과정이다.

 

 

kernel aggregation을 하는 이유는 당연히 이게 더 효율적인 방식이기 때문이다. 논문의 아래 부분을 참조하면 된다.

 

 

3. Training Deep DY-CNNs

 

저자들은 자신들의 dynamic convolution layer을 이용한 DY-CNN이 훈련하기가 까다롭다고 하는데, 이는 당연히 K개의 kernel들에 대해서 모두 joint optimization을 해주어야하기 때문이다. 훈련을 좀 더 쉽고 효과적으로 하기 위해 저자들은 2가지 insight를 소개한다.

 

Insight 1. Sum the Attention to 1

 

말 그대로 attention 가중치들을 전부 더한 것이 1이 되도록 만드는 것이다. 

 

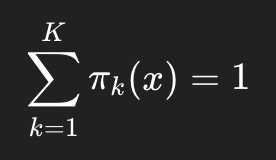
이 조건을 추가해주는 것인데, 이는 dynamic perceptron에 대한 논문의 s.t.에서도 확인할 수 있다.

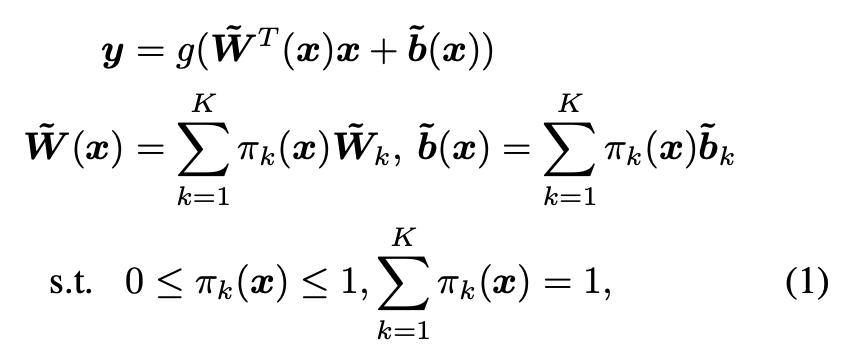
위에 보면, attention 가중치가 0에서 1 사이의 범위를 가져야한다는 조건은 CondConv라는 방법론이 먼저 내세운 조건이고, 저자들은 여기서 한 발자국 더 나아가 다 합쳐서 1이 되어야한다는 조건까지 추가한 것이다.

 

왜 이게 optimization에 도움이 될까?

 

아래 그림을 한 번 보자.

 

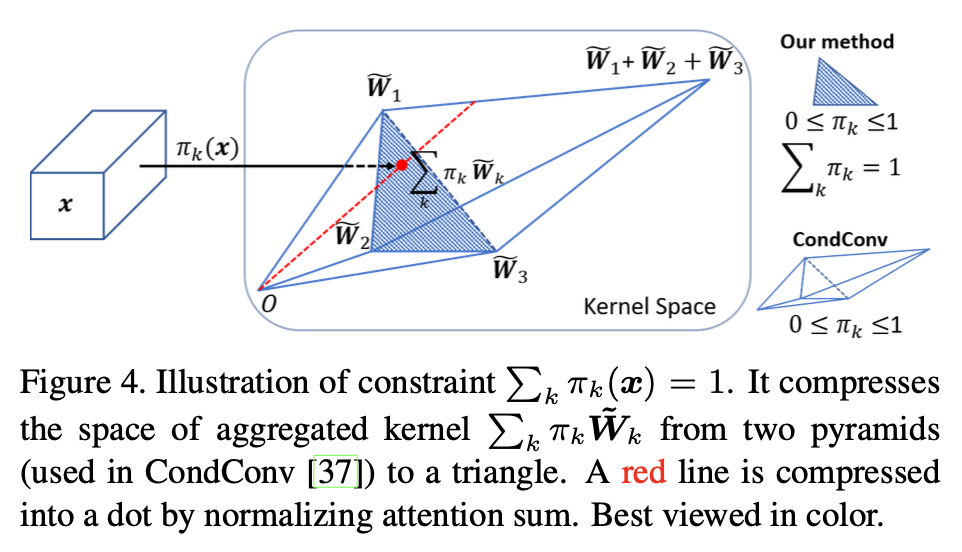
일단 우선적으로 이 그림이 의미하는 것은, 저자들이 제시하는 "다 합쳐서 1이 되도록" 이라는 조건을 달면 kernel space가 그저 평면의 삼각형 모양으로 compress 된다는 것이다. 앞서 말했던 CondConv의 조건인 "0에서 1사이의 값을 가지도록" 만 적용한다면, 저렇게 3D parallelepiped—a “two-pyramid” shape 가 나오게 된다.

 

위 그림에 대한 좀 더 자세한 설명은, 학습된 커널 3개 (W1, W2, W3)이 어떤 high-dimensional space에 점으로 있다고 보고, 가중치가 0~1 사이에 있다는 조건만 있을 때, kernel space의 모양이 저 이상하게 생긴 3d 도형이다. kernel들의 모든 경우의 수 이런 느낌이라고 생각하면 좋을 것 같다.

 

하지만 "합쳐서 1" 의 조건을 적용하면 우리의 새로운 aggregated kernel이 항상 W1, W2, W3 커널들의 convex combination이 된다. 그래서 더이상 3D 도형이 아닌, W1, W2, W3을 꼭지점으로 하는 삼각형으로 kernel space가 줄어들게 된다. 3D에서 2D로 kernel space가 줄어들었기에 가중치 π들의 학습이 더 쉬워지는 것이다.

 

좀 더 자세히 설명하자면, 저 빨간 선의 공간이 더이상 선이 아니라 쫙 압축되면서 점으로 되는 것이다. 매우 직관적으로 말해서, 저 높이의 부분들이 평면으로 찌부된다고 보면 된다.

 

Insight 2. Near-Uniform Attention in Early Training Epochs

 

훈련의 초기 단계에서 attention의 distribution을 일부러 flatten하는 것이다. 이걸 어떻게 flatten하냐? Softmax의 temperature를 높게 세팅해주면 된다 (e.g. 타우를 30으로). 훈련의 초기 단계가 지나면 타우를 다시 30에서 1로 돌린다.

 

저자들의 이 부분 서술을 같이 보자.

 

일단 Softmax with temperature는 위에 보는 것처럼 일반적인 softmax가 아닌 exp() 안의 분모에 타우가 들어간 꼴이다. 

 

타우가 증가하면 할 수록 output이 uniform distribution에 가까워진다. 그래서 저자들은 초반 단계에 높은 타우를 이용해 각 attention에 어느 정도에 값이 들어갈 수 있게 initialize한다고 볼 수 있다. 그냥 softmax를 취해버리면 처음부터 한 개의 attention 값은 거의 1, 나머지는 전부 거의 0 이런 식으로 될텐데, 그렇게 되면 0이 되버린 attention들은 gradient 학습이 안되어서 죽어버린다. 이를 초기에 방지하고자 미리 attention 값을 좀 쌓아놓고 얘네들이 "healthy" 한 gradient를 골고루 받을 수 있게끔 해주는 것이다.

 

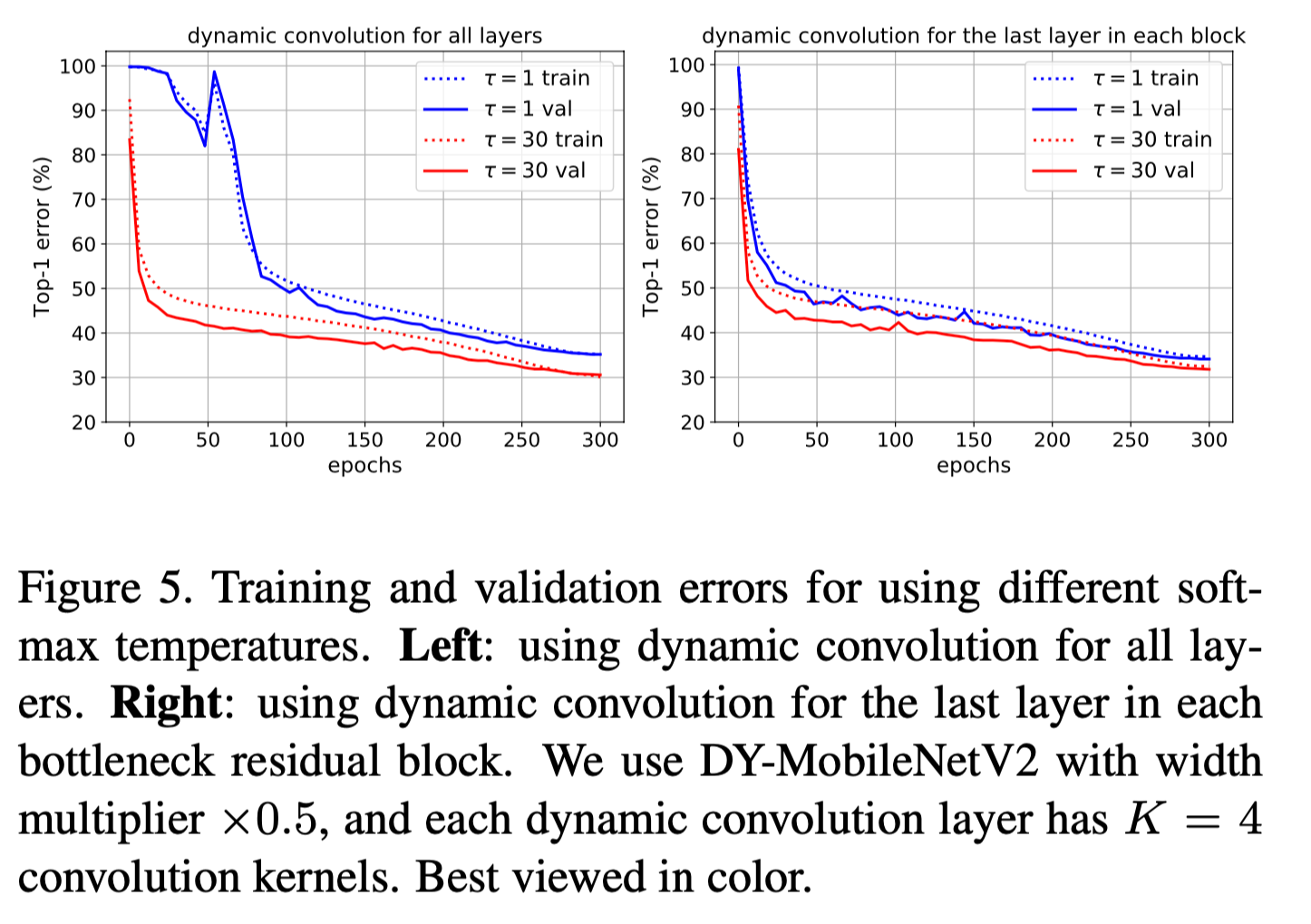
결과는 잘 나오는 것을 볼 수 있고, 다음과 같이 된다.

 

 

4. Results and Discussion

 

결국 DY-CNN은 작은 amount의 computational cost를 더하는 대신에 performance의 significant한 boost를 이뤄내는 것이다.

 

위의 그림처럼 Dynamic이 들어간 애들이 x축 기준 오른쪽으로는 조금 더 가있으나(more computational cost) 이에 비해 위로 훨씬 더 많이 올라가는 것을 볼 수 있다(ImageNet Accuracy).

 

이를 더 정리하자면, 많은 커널들의 사용으로 매우 많이 늘어난 parameter 수, 매우 조금이지만 늘어난 computational cost, 그리고 이에 비해 많이 늘어난 성능 이라고 할 수 있다.