LSTM은 기존의 Vanilla RNN이 long-term memory에 취약하다는 단점을 보완하기 위해 나온 아키텍처이다. 기존의 RNN은 동일한 weight와 구조로 layer가 계속 반복되다 보니 vanishing gradient / exploding gradient 문제가 있었고, 이로 인한 long-term memory를 기억하는 데에 문제가 생기게 된다.
LSTM은 큰 틀에서 이 문제를 short-term memory가 flow 할 수 있게 하는 path, long-term memory가 flow 할 수 있게 하는 path를 구분하여 두면서 해결하고자 하였다.
LSTM의 해결책
LSTM의 구조에 대한 가장 유명한 그림이다. 중간에 구조들이 보이는 것이 하나의 LSTM block이고, 이러한 block들이 RNN과 마찬가지로 연속해서 반복되는 구조이다.
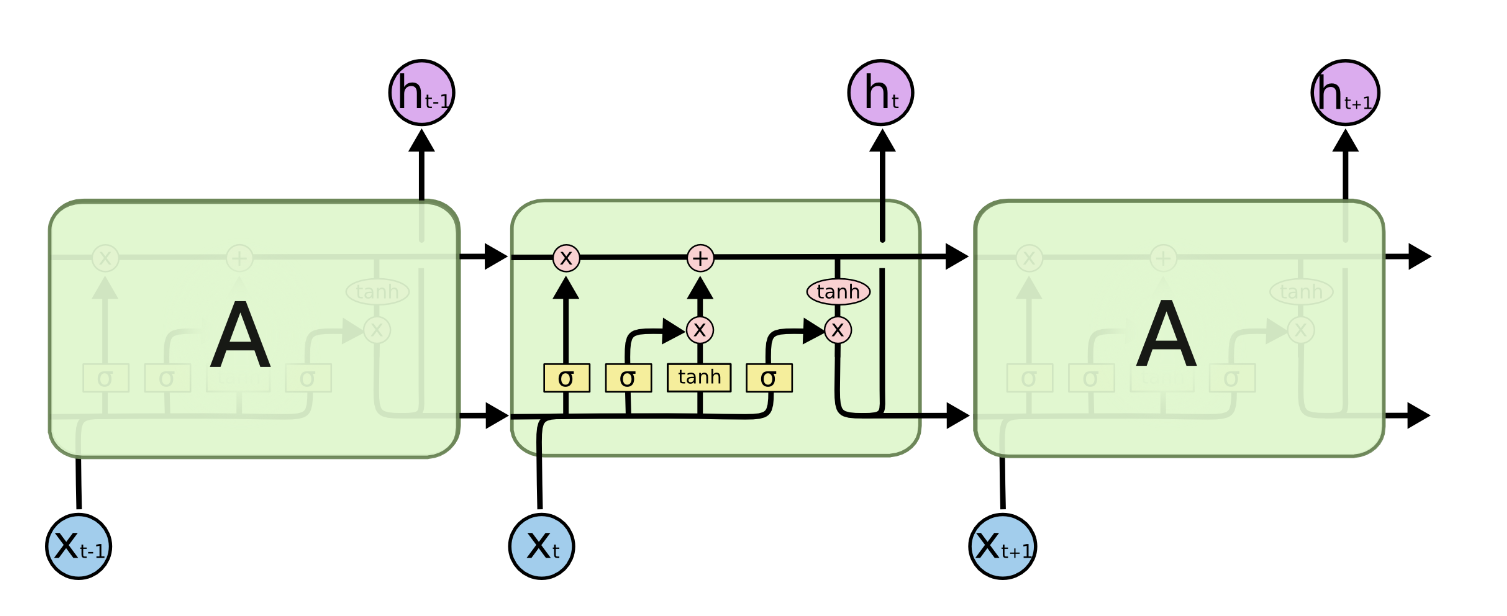
우선, 위에서 얘기한 RNN의 단점인 vanishing / exploding gradient에 관한 부분과 long-term memory에 대한 path를 구분지어 놓았다는 점부터 다뤄보자.

이 C 들은 Cell state라고 하고, long-term memory를 담당한다. 그리고 바로 이 부분이 LSTM의 key idea이다. RNN에게서 문제점들이 발생했던 이유는 이전 정보들에 지속적으로 weight들이 곱해지면서 그 weight가 1보다 클 경우 exponentially increase / weight가 1보다 작을 경우 exponentially decrease가 되는 것이다. LSTM을 처음 소개한 저자들의 언급을 보자.

하지만 위의 Cell state를 보면 하나의 숫자로 쭉 흐르는 것을 볼 수 있다. C에 minor한 linear interaction들만 가해질 뿐, 여러 번의 layer를 거친다고 해서 exponentially increase 하거나 decrease 하지 않는 모습을 보여준다. LSTM은 이렇게 따로 Cell state를 둠으로써 long-term memory가 쉽게 flow through the network 하게 만들어준다.
LSTM의 구조 단계별 설명
LSTM의 구조는 3개의 gate로 이루어져 있다. 하지만 이 gate들의 이름을 미리 말하고 설명하는 것보다 아래의 사진을 통한 이해가 훨씬 머리에 잘 들어오는 것 같아 구조에 대한 설명 후 용어 정리를 하려 한다. 결국은 용어가 중요한게 아니라 어떤 기능을 하는지 머리에 남기는게 더 중요하지 않을까.

1. 이전 메모리를 얼마나 보존할 것인가?
처음부터 차근차근 짚어보도록 하자.

LSTM의 첫 단계는 바로 이전의 long-term memory, 즉 ((C_{t-1})) 을 얼마나 보존하고 갈 것인지에 대한 부분이다. 왜 그런 원리냐면, 바로 Sigmoid 함수 때문이다. Sigmoid 함수는 input으로 들어온 숫자를, 어떤 숫자가 들어오던 간에 0 ~ 1 사이로 변환해주는 함수이다. 0 ~ 1 사이의 숫자가 나온다는 것은 어떤 퍼센트지가 나온다는 것과 동일한 뜻이다.
그래서 short-term memory (1) 와 그 weight (2.70) 가 곱해지고, Input (1) 과 그 weight (1.63) 가 곱해지며, 이 두 개가 sum으로 더해진다. 그리고 sum 이후 bias (1.62)가 더해지면서 이 결과물이 통째로 sigmoid 함수로 들어가서 long-term memory를 몇 퍼센트 정도 보존할 건지에 대한 숫자가 0 ~ 1 사이로 나오는 것이다. 현재 Input이 1인 상황에서는 2인 long-term memory를 아주 살짝 (1.99) 줄여주는 효과가 있어보인다.
이 과정을 수식으로 나타낸 것이 바로 다음 사진이다.

이전의 long-term memory를 얼마나 보존할 지는 short-term memory와 현재의 input 값에 따라 달라진다. 이번에는 input이 -10 이라고 해보자.

input이 -10일 경우에는 sigmoid 함수를 거쳐서 나온 값이 0이 되므로 2 x 0으로 이전의 long-term memory를 전혀 보존하지 않게 된다. 이후에도 다루겠지만, LSTM에서 sigmoid 함수가 들어가는 부분은 모두 정보를 몇 퍼센트 보존할 것인지에 대한 부분이라고 생각하면 된다.
이 첫 단계가 바로 Forget gate이다.
2. Long-term memory에 무엇을, 얼마나 추가할 것인가?
LSTM의 그 다음 단계는 long-term memory에
1. 무엇을 추가할 것인가?
2. 그걸 얼마나 추가할 것인가?
를 결정하는 단계이다.
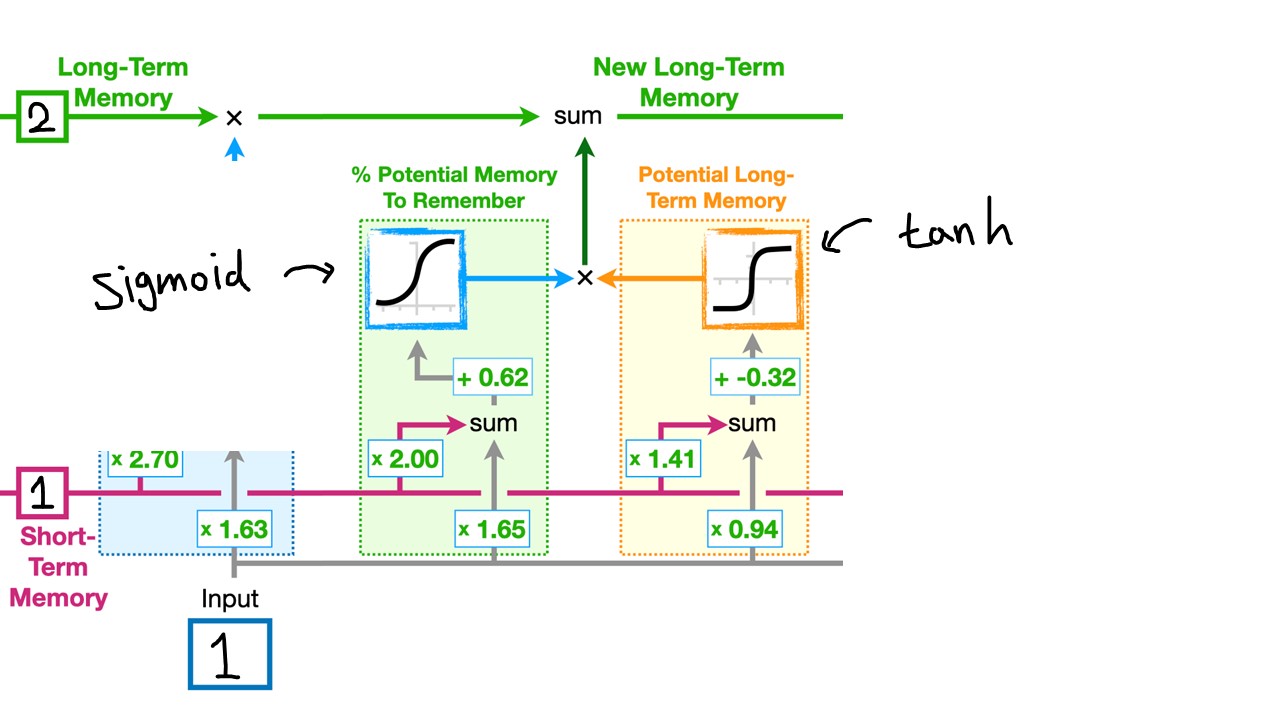
오른쪽의 주황색 블록: 무엇을 추가할 것인가?
왼쪽의 초록색 블록: 그걸 얼마나 추가할 것인가?
에 해당하는 부분이다.
오른쪽의 주황색 블록에서는 Potential long-term memory, 즉 이번 timestep에서 long-term memory에 추가할 잠재적인 후보 정보들을 계산하는 것이다. Short-term memory (1) 과 그 weight (1.41) 을 곱하고, input과 그 weight (0.94) 를 곱하여 또 더해준다. 그리고 bias (-0.32) 를 더해주고, 이걸 tanh 함수에 넣어준다. Tanh 함수는 0 ~ 1 사이의 값을 내주는 sigmoid 대신, input에 어떤 숫자가 들어오던 -1 ~ 1 사이의 값을 출력한다. 결국 이 부분에서는 input과 short-term memory를 조합해서 -1 ~ 1 사이의 potential memory를 생성하는 부분이다. 아까 sigmoid처럼, LSTM에서 tanh 함수를 본다면 새로운 정보를 만들어내는 것과 관련이 있다고 생각하면 된다.
왼쪽의 초록색 블록에서는 주황색 블록에서 생성한 잠재적인 long-term memory 후보를 몇 퍼센트 정도 실제로 long-term memory에 반영할지를 결정하는 부분이다. 직관적으로만 보아도 밑에 뭔가 short-term memory와 input이 조합되고 또 sigmoid 함수를 통과하고, 이 값이 주황색 블록에서 나온 값에 곱해진다 (x 표시 주목). 나온 값에다가 퍼센트지를 곱해주는 것이다. 방법은 동일하므로 사진을 보고 숫자를 따라가면 될 것이다.
이렇게 나온 결과는 흘러들어온 Cell state에 더해주며 New cell state가 된다.
이 과정을 수식으로 나타낸 것이 바로 다음 사진이다.

물결 ((C_t))가 잠재적 long-term memory, 그리고 ((i_t))가 그 퍼센트지를 의미하는 것이다.
이 두 번째 단계가 바로 Input gate이다.
3. Short-term memory를 얼마나 업데이트 할 것인가?
LSTM의 마지막 단계는 short-term memory를 업데이트 하는 부분이다.

아까와 마찬가지로
오른쪽의 분홍색 블록: potential short-term memory를 만들어내는 부분
왼쪽의 보라색 블록: potential short-term memory 중 몇 퍼센트나 보존할 것인가?
에 관한 내용이다. 마찬가지로 sigmoid와 tanh 함수가 각각 보이는데, tanh로 정보를 만들어내고 sigmoid로 그 비중을 조절하는 것이다. 분홍색 블록을 먼저 보면, potential short-term memory는 업데이트 된 new long-term memory에서 일단 가져온 후 tanh에 태우는 것을 볼 수 있다.
그 후 보라색 블록에서 기존의 short-term memory와 input, bias를 잘 조합하여 sigmoid에 태워 몇 퍼센트지를 보존할 지 0 ~ 1 사이의 값을 내보낸 후, 이 값고 분홍색 블록에서 tanh에 태웠던 potential short-term memory와 곱해주면 업데이트 된 new short-term memory가 완성이 되고, 이는 Cell state와 함께 LSTM의 최종 output이 된다.
이 과정을 수식으로 나타낸 것이 바로 다음 사진이다.

sigmoid를 태운 ((o_{t}))가 tanh를 채운 cell state에 곱해지면서 새로운 hidden state (short-term memory) 로 output이 되는 것을 볼 수 있다.
LSTM이 정말 유명함에도 불구하고 상대적으로 복잡해 보이는 구조로 인해서 항상 얘기할 때 기억이 잘 나지 않았는데, 이렇게
1. 기존 장기 기억 정보를 얼마나 가져갈 것이냐 조절 부분
2. 새로운 장기 기억 정보를 만들고 그걸 얼마나 가져갈 것이냐 부분
3. 새로운 단기 기억 정보를 만들고 그걸 얼마나 가져갈 것이냐 부분
이렇게 직관적으로 이해할 수 있는 설명인 것 같아 유익한 것 같다.
